题目内容
已知△ABC,D,E,F分别是AB,BC,CA的中点,设
=
,
=
,则
+
是( )
| AB |
| a |
| AC |
| b |
| DE |
| DF |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
考点:*平面向量
专题:
分析:首先根据题意画出图形,然后由三角形法则求得
的长,又由D,E,F分别是AB,BC,CA的中点,利用三角形中位线的性质,求得
与
,继而求得答案.
| BC |
| DE |
| DF |
解答:
 解:如图,∵
解:如图,∵
=
,
=
,
∴
=
-
=
-
,
∵D,E,F分别是AB,BC,CA的中点,
∴
=
=
,
=
=
-
,
∴
+
=-
+
.
故选B.
 解:如图,∵
解:如图,∵| AB |
| a |
| AC |
| b |
∴
| BC |
| AC |
| AB |
| b |
| a |
∵D,E,F分别是AB,BC,CA的中点,
∴
| DE |
| 1 |
| 2 |
| AC |
| 1 |
| 2 |
| b |
| DF |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| a |
∴
| DE |
| DF |
| 1 |
| 2 |
| a |
| b |
故选B.
点评:此题考查了平面向量的知识.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图的正方体截去一部分后,剩下的几何体的面数和棱数分别为( )
如图的正方体截去一部分后,剩下的几何体的面数和棱数分别为( )| A、6,13 | B、7,15 |
| C、6,15 | D、7,14 |
地图上的距离为10厘米,这张地图的比例尺为1:100000,则两地的实际距离是( )
| A、100米 |
| B、1000米 |
| C、10000米 |
| D、100000米 |
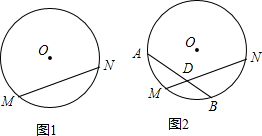 如图1,已知⊙O的弦MN所对的弧是120°,圆心O到MN所在的直线的距离是4.
如图1,已知⊙O的弦MN所对的弧是120°,圆心O到MN所在的直线的距离是4.
 已知线段AB,延长AB到点C,使AB=3BC,则
已知线段AB,延长AB到点C,使AB=3BC,则