题目内容
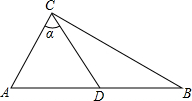 已知如图,Rt△ABC中,∠ACB=90°,D是AB的中点,sinα=
已知如图,Rt△ABC中,∠ACB=90°,D是AB的中点,sinα=| 2 |
| 3 |
| 5 |
考点:解直角三角形
专题:计算题
分析:作DE⊥BC于E,如图,则DE∥AC,根据平行线的性质得∠CDE=∠ACD=α,由于D是AB的中点,则DE为△ABC的中位线,根据三角形中位线的性质得到DE=
AC=2
,CE=BE,在Rt△CDE中,利用正弦的定义得到sin∠CDE=
=
,则可设CE=2a,CD=3a,利用勾股定理得DE=
a,则
a=2
,解得a=2,可计算出BC=2CE=8,然后根据三角形面积公式求解.
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| CE |
| CD |
| 5 |
| 5 |
| 5 |
解答: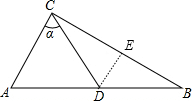 解:作DE⊥BC于E,如图,
解:作DE⊥BC于E,如图,
∵∠ACB=90°,
∴DE∥AC,
∴∠CDE=∠ACD=α,
∵D是AB的中点,
∴DE为△ABC的中位线,
∴DE=
AC=2
,CE=BE,
在Rt△CDE中,sin∠CDE=sinα=
=
,
设CE=2a,CD=3a,
∴DE=
=
a,
∴
a=2
,解得a=2,
∴CE=4,
∴BC=2CE=8,
∴S△ABC=
AC•BC=
×4
×8=16
.
 解:作DE⊥BC于E,如图,
解:作DE⊥BC于E,如图,∵∠ACB=90°,
∴DE∥AC,
∴∠CDE=∠ACD=α,
∵D是AB的中点,
∴DE为△ABC的中位线,
∴DE=
| 1 |
| 2 |
| 5 |
在Rt△CDE中,sin∠CDE=sinα=
| 2 |
| 3 |
| CE |
| CD |
设CE=2a,CD=3a,
∴DE=
| CD2-CE2 |
| 5 |
∴
| 5 |
| 5 |
∴CE=4,
∴BC=2CE=8,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
已知α为锐角,下列不等式中正确的是( )
①tanα>1;②0<sinα<1;③cotα<1;④0<cosα<1.
①tanα>1;②0<sinα<1;③cotα<1;④0<cosα<1.
| A、② | B、①,②,③ |
| C、②,④ | D、①,②,③,④ |
下列说法:①等腰三角形的高、中线、角平分线互相重合;②等腰三角形的两腰上的中线长相等;③等腰三角形的腰一定大于其腰上的高;④等腰三角形的一边长为8,一边长为16,那么它的周长是32或40.其中不正确的( )
| A、①③ | B、①④ |
| C、①③④ | D、①②③④ |
一条线段的黄金分割点有( )
| A、1个 | B、2个 | C、3个 | D、无数个 |