题目内容
解方程组:
.
|
考点:高次方程
专题:
分析:将第二个方程运用因式分解法转化为两个二元一次方程,分别与第一个方程组合成两个新的二元二次方程组问题即可解决.
解答:解:
,
由②得:( x+3x+2y)(x-3x-2y)=0,
∴4x+2y=0③,或-2x-2y=0④;
由③得:y=-2x,代入①并化简得:x2=2;
∴x=±
,y=±2
;
由④得:y=-x,代入①并化简得:x2=5,
∴x=±
,y=±
;
∴原方程组的解为:
,
,
,
.
|
由②得:( x+3x+2y)(x-3x-2y)=0,
∴4x+2y=0③,或-2x-2y=0④;
由③得:y=-2x,代入①并化简得:x2=2;
∴x=±
| 2 |
| 2 |
由④得:y=-x,代入①并化简得:x2=5,
∴x=±
| 5 |
| 5 |
∴原方程组的解为:
|
|
|
|
点评:本题考查了高次方程的解法问题;解题的关键是运用因式分解法将高次方程转化为低次方程,进而求解即可.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
若a+b+c=0,那么一元二次方程ax2+bx+c=0必有一根是( )
| A、O | B、1 | C、-1 | D、2 |
若一个等腰三角形两边长分别是x2-12x+32=0的两根,则这个等腰三角形的周长为( )
| A、20 | B、16 |
| C、16或20 | D、不能确定 |
下列说法中,结论错误的是( )
| A、直径相等的两个圆是等圆 |
| B、三角形的外心是这个三角形三条角平分线的交点 |
| C、圆中最长的弦是直径 |
| D、一条弦把圆分成两条弧,这两条弧可能是等弧 |
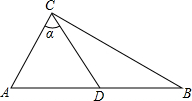 已知如图,Rt△ABC中,∠ACB=90°,D是AB的中点,sinα=
已知如图,Rt△ABC中,∠ACB=90°,D是AB的中点,sinα=