题目内容
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映,如调整价格,每涨价1元,每星期要少卖出8件,每降价1元,每星期多卖12件,已知商品进价为每件40元,问如何定价才能使利润最大?
考点:二次函数的应用
专题:销售问题
分析:设出涨价或降价x元以后,准确表示出每件的盈利及每星期的销售量,利用盈利公式:利润=每件盈利×销售量,借助函数的性质问题即可解决.
解答:解:设每件涨价为x元时获得的总利润为y元.
此时每件盈利60-40+x=20+x(元),销售量为300-8x(件);
∴y=(20+x)(300-8x)
=-8x2+140x+6000
∵a=-8<0,
∴当x=-
=8.75时,y取得最大值,
此时y=
=6000+612.5
=6612.5
即定价为60+8.75=77.5元时,才能使利润最大;
设每件降价x元时的总利润为y元.
此时每件盈利60-40-x=20-x(元),销售量为300+12x(件);
∴y=(20-x)(300+12x)=-12x2-60x+6000
∵a=-12<0,
∴当x=-
=-2.5时,y取得最大值,
此时y=
=6075;
即定价为60-2.5=57.5(元)时利润最大,最大值为6075元.
综合所述,定价为77.5元时可获得最大利润,最大利润为6612.5元.
此时每件盈利60-40+x=20+x(元),销售量为300-8x(件);
∴y=(20+x)(300-8x)
=-8x2+140x+6000
∵a=-8<0,
∴当x=-
| 140 |
| 2×(-8) |
此时y=
| 4×(-8)×6000-1402 |
| 4×(-8) |
=6000+612.5
=6612.5
即定价为60+8.75=77.5元时,才能使利润最大;
设每件降价x元时的总利润为y元.
此时每件盈利60-40-x=20-x(元),销售量为300+12x(件);
∴y=(20-x)(300+12x)=-12x2-60x+6000
∵a=-12<0,
∴当x=-
| -60 |
| 2×(-12) |
此时y=
| 4×(-12)×6000-(-60)2 |
| 4×(-12) |
即定价为60-2.5=57.5(元)时利润最大,最大值为6075元.
综合所述,定价为77.5元时可获得最大利润,最大利润为6612.5元.
点评:考查了二次函数在现实生活中的实际应用问题;解题的关键是将实际问题转化为二次函数问题后,准确列出二次函数关系式,灵活运用二次函数性质来解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若a+b+c=0,那么一元二次方程ax2+bx+c=0必有一根是( )
| A、O | B、1 | C、-1 | D、2 |
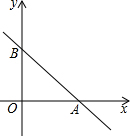 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A、B,则△OAB为此函数的坐标三角形.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A、B,则△OAB为此函数的坐标三角形.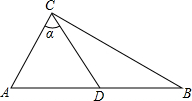 已知如图,Rt△ABC中,∠ACB=90°,D是AB的中点,sinα=
已知如图,Rt△ABC中,∠ACB=90°,D是AB的中点,sinα=