题目内容
2. 如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO的度数是( )
如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO的度数是( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
分析 首先求出∠HDB的度数,再利用直角三角形斜边中线定理可得OH=OD,由此可得∠OHD=∠ODH即可解决问题.
解答 解: ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∵AC⊥BD,DO=OB,∠DAO=∠BAO=25°,
∴∠ABO=90°-∠BAO=65°,
∵DH⊥AB,
∴∠DHB=90°,
∴∠BDH=90°-ABO=25°,
在Rt△DHB中,∵OD=OB,
∴OH=OD=OB,
∴∠DHO=∠HDB=25°,
故选B.
点评 本题考查菱形的性质,直角三角形斜边中线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
12.从一个多边形的一个顶点出发,可以画出7条对角线,则这个多边形的边数为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
10.用科学记数法表示的数3.61×108.它的原数是( )
| A. | 36100000000 | B. | 3610000000 | C. | 361000000 | D. | 36100000 |
17.有15张大小、形状及背面完全相同的卡片,卡片正面分别画有正三角形、正方形、圆,从这15张卡片中任意抽取一张正面的图形既是轴对称图形,又是中心对称图形的概率是$\frac{2}{3}$,则正面画有正三角形的卡片张数为( )
| A. | 3 | B. | 5 | C. | 10 | D. | 15 |
7. 一个空心的圆柱如图所示,则它的俯视图是( )
一个空心的圆柱如图所示,则它的俯视图是( )
 一个空心的圆柱如图所示,则它的俯视图是( )
一个空心的圆柱如图所示,则它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
14. 已知有理数a、b、c在数轴上的位置如图所示,下列子正确的是( )
已知有理数a、b、c在数轴上的位置如图所示,下列子正确的是( )
 已知有理数a、b、c在数轴上的位置如图所示,下列子正确的是( )
已知有理数a、b、c在数轴上的位置如图所示,下列子正确的是( )| A. | cb>ab | B. | ac>ab | C. | cb<ab | D. | c+b>a+b |
12.已知实数x1,x2满足x1+x2=11,x1x2=30,则以x1,x2为根的一元二次方程是( )
| A. | x2-11x+30=0 | B. | x2+11x+30=0 | C. | x2+11x-30=0 | D. | x2-11x-30=0 |
 已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.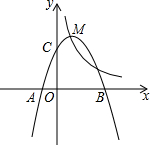 如图,抛物线y=-(x-h)(x-h+2)(h为常数)交x轴于A,B两点(点A在点B左侧),交y轴于点C,顶点为M,
如图,抛物线y=-(x-h)(x-h+2)(h为常数)交x轴于A,B两点(点A在点B左侧),交y轴于点C,顶点为M,