题目内容
16.基础巩固:(1)计算:($\frac{1}{2}$)-1-3(π-3.14)0-$\frac{\sqrt{3}}{2}$+2$\sqrt{3}$+|$\frac{\sqrt{3}}{2}$-1|.
(2)先化简,再求代数式(1-$\frac{3}{x+2}$)÷$\frac{{x}^{2}-1}{x+2}$的值,其中x=$\sqrt{3}$-1.
分析 (1)直接利用负指数幂的性质以及零指数幂的性质和绝对值的性质分别化简得出答案;
(2)首先计算括号里面,进而利用分式混合运算法则化简,再把已知代入求出答案.
解答 解:(1)($\frac{1}{2}$)-1-3(π-3.14)0-$\frac{\sqrt{3}}{2}$+2$\sqrt{3}$+|$\frac{\sqrt{3}}{2}$-1|
=2-3-$\frac{\sqrt{3}}{2}$+2$\sqrt{3}$+1-$\frac{\sqrt{3}}{2}$
=$\sqrt{3}$;
(2)(1-$\frac{3}{x+2}$)÷$\frac{{x}^{2}-1}{x+2}$
=($\frac{x+2}{x+2}$-$\frac{3}{x+2}$)×$\frac{x+2}{(x+1)(x-1)}$
=$\frac{x-1}{x+2}$×$\frac{x+2}{(x+1)(x-1)}$
=$\frac{1}{x+1}$
把x=$\sqrt{3}$-1代入上式可得:
原式=$\frac{1}{\sqrt{3}-1+1}$=$\frac{\sqrt{3}}{3}$.
点评 此题主要考查了二次根式的加减运算以及实数运算和分式的化简求值,正确化简分式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列图中不是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
4.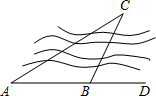 如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )
如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )
 如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )
如图,要测量凉亭C到河岸AD的距离,在河岸相距200米的A,B两点,分别测得∠CAB=30°,∠CBD=60°,则凉亭C到河岸AD的距离为( )| A. | 100米 | B. | 100$\sqrt{3}$米 | C. | 200米 | D. | 200$\sqrt{3}$米 |
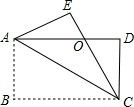 如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O. 画出下列几何体的三视图.
画出下列几何体的三视图.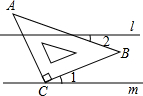 如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的和是多少度?并证明你的结论.
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的和是多少度?并证明你的结论.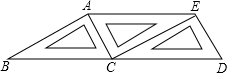 如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )
如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )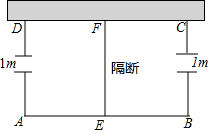 如图所示,利用一面墙(墙的长度足够),用篱笆围成一个形如矩形ABCD的场地,在AD,BC边上各有一个宽为1m的缺口,在场地中有用篱笆做的隔断EF,且EF⊥AB,AB>EF,已知所用篱笆总长度为38m.
如图所示,利用一面墙(墙的长度足够),用篱笆围成一个形如矩形ABCD的场地,在AD,BC边上各有一个宽为1m的缺口,在场地中有用篱笆做的隔断EF,且EF⊥AB,AB>EF,已知所用篱笆总长度为38m.