题目内容
9.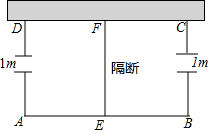 如图所示,利用一面墙(墙的长度足够),用篱笆围成一个形如矩形ABCD的场地,在AD,BC边上各有一个宽为1m的缺口,在场地中有用篱笆做的隔断EF,且EF⊥AB,AB>EF,已知所用篱笆总长度为38m.
如图所示,利用一面墙(墙的长度足够),用篱笆围成一个形如矩形ABCD的场地,在AD,BC边上各有一个宽为1m的缺口,在场地中有用篱笆做的隔断EF,且EF⊥AB,AB>EF,已知所用篱笆总长度为38m.(1)设隔断EF的长为x(m),请用含x的代数式表示AB的长.
(2)所围成形如矩形ABCD的场地的面积为100m2时,求AB的长.
(3)所围成矩形ABCD场地的面积能否为140m2?若能,求AB的长;若不能,说明理由.并写出所围成的矩形ABCD场地面积的最大值.
分析 (1)根据题意可得AB=38-3x+2,即可得出答案;
(2)利用矩形面积公式得出S=100,进而得出答案;
(3)利用矩形面积公式得出S=140,再利用利用配方法即可求出函数最大值.
解答 解:(1)设隔断EF的长为x(m),
则AB=38-3x+2=40-3x;
(2)由题意可得:S=x(40-3x)=100,
整理得:-3x2+40x-100=0,
则3x2-40x+100=0
解得:x1=10,x2=$\frac{10}{3}$,
当EF=10m,则AB=40-30=10(m),
此时EF=AB,不合题意,
故x=$\frac{10}{3}$,则AB=40-3×$\frac{10}{3}$=30(m),
答:AB的长为30m;
(3)当S=140m2,
则x(40-3x)=140,
整理得:3x2-40x+140=0,
则△=b2-4ac=1600-1680=-80<0,
故所围成矩形ABCD场地的面积不能为140m2,
S=x(40-3x)=-3x2+40x
=-3(x2-$\frac{40}{3}$x)
=-3(x-$\frac{20}{3}$)2+$\frac{400}{3}$,
当x=$\frac{20}{3}$时,所围成的矩形ABCD场地面积的最大值为:$\frac{400}{3}$m2.
点评 本题考查了二次函数的应用,解答本题的关键是结合题意利用长方形的面积列出函数关系式并掌握求二次函数最值的方法.

练习册系列答案
相关题目
17.下面四个汽车标志图案是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.下列一元一次方程中,解为x=-3的是( )
| A. | 2x+3=-6 | B. | 2x-6=0 | C. | x+3=0 | D. | 5x-14=1 |
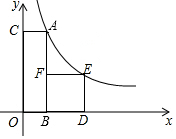 如图,四边形ABOC是矩形,BDEF是正方形.点B、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点A、E在反比例函数y=$\frac{4t}{x}$的图象上,且AB=4AC,若正方形BDEF的面积为S,则S关于t的函数图象是( )
如图,四边形ABOC是矩形,BDEF是正方形.点B、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点A、E在反比例函数y=$\frac{4t}{x}$的图象上,且AB=4AC,若正方形BDEF的面积为S,则S关于t的函数图象是( )