题目内容
17.在平面直角坐标系中,把点P(-5,3)向右平移8个单位得到点P1,再将点P1绕原点顺时针旋转90°得到点P2,则点P2的坐标是( )| A. | (3,3)或(-3,-3) | B. | (-3,3) | C. | (3,-3) | D. | (3,-3)或(-3,3) |
分析 先根据题意求出P1的坐标,然后旋转作出P2的坐标,根据旋转的性质即可求出点P2的坐标
解答  解:∵P(-5,3),
解:∵P(-5,3),
∴把点P(-5,3)向右平移8个单位得到点P1为(3,3),
∴P1O与x轴正半轴的夹角为45°,
∵P2O⊥P1O,
∴P2O与x轴正半轴的夹角为45°,
∴P1与P2关于x轴对称,
∴P2的坐标为(3,-3),
故选(C)
点评 本题考查旋转与平移的性质,解题的关键是正确画出图形,然后根据条件分析变换前后的坐标变化,本题属于基础题型.

练习册系列答案
相关题目
12.下列命题中,为真命题的是( )
| A. | 对顶角相等 | B. | 同位角相等 | ||
| C. | 若a2=b2,则a=b | D. | 同旁内角相等,两直线平行 |
 已知,如图所示,在长方形ABCD中,AB=4,BC=3.
已知,如图所示,在长方形ABCD中,AB=4,BC=3.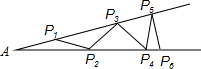 课本“目标与评定”中有这样一道思考题,如图钢架中,∠A=20°,焊上等长的钢条来加固钢架,若AP1=P1P2,问这样的钢条至多需要多少根?
课本“目标与评定”中有这样一道思考题,如图钢架中,∠A=20°,焊上等长的钢条来加固钢架,若AP1=P1P2,问这样的钢条至多需要多少根?