题目内容
如图,∠ABC=∠A′B′C′,BD、B′D′分别是∠ABC、∠A′B′C′的平分线,求证:∠1=∠2.
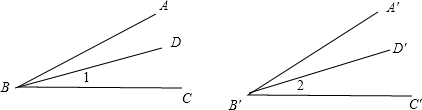
证明:∵BD,B′D′分别是∠ABC,∠A′B′C′的平分线
∴∠1=
∠ABC,∠2= ( )
又∵∠ABC=∠A′B′C′
∴
∠ABC=
∠A′B′C′
∴∠1=∠2( ).
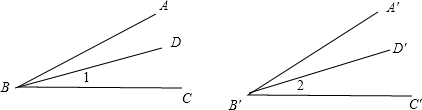
证明:∵BD,B′D′分别是∠ABC,∠A′B′C′的平分线
∴∠1=
| 1 |
| 2 |
又∵∠ABC=∠A′B′C′
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2(
考点:角平分线的定义
专题:推理填空题
分析:根据角平分线的定义,可得出∠1,∠2分别为∠ABC,∠A′B′C′的一半,再由∠ABC=∠A′B′C′即可得出答案.
解答:解:∵BD、B′D′分别是∠ABC、∠A′B′C′的平分线,
∴∠1=
∠ABC,∠2=
∠A′B′C′,
∵∠ABC=∠A′B′C′
∴∠1=∠2.
故答案为:
∠A′B′C′,角平分线的定义,等量代换.
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC=∠A′B′C′
∴∠1=∠2.
故答案为:
| 1 |
| 2 |
点评:本题考查了角平分线的定义,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在菱形ABCD中,点Q是对角线DB上一点,连接CQ并延长,交AD于点E,交BA的延长线于点F,连接AQ.
在菱形ABCD中,点Q是对角线DB上一点,连接CQ并延长,交AD于点E,交BA的延长线于点F,连接AQ.