题目内容
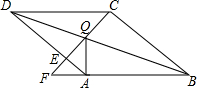 在菱形ABCD中,点Q是对角线DB上一点,连接CQ并延长,交AD于点E,交BA的延长线于点F,连接AQ.
在菱形ABCD中,点Q是对角线DB上一点,连接CQ并延长,交AD于点E,交BA的延长线于点F,连接AQ.(1)求证:∠QAD=∠QCD;
(2)若菱形的边长为2,QF=2CQ,QA⊥FB,求BQ的长.
考点:菱形的性质,全等三角形的判定与性质
专题:
分析:(1)根据菱形性质得出DC=AD,∠CDQ=∠ADQ,根据SAS推出△CDQ≌△ADQ即可;
(2)证△DQC∽△BQF,求出CQ的长,求出AQ长,根据勾股定理即可求出答案.
(2)证△DQC∽△BQF,求出CQ的长,求出AQ长,根据勾股定理即可求出答案.
解答:(1)证明:∵四边形ABCD是菱形,
∴DC=AD,∠CDQ=∠ADQ,
在△CDQ和△ADQ中
∴△CDQ≌△ADQ(SAS),
∴∠QAD=∠QCD;
(2)解:∵四边形ABCD是菱形,
∴DC=AB=2,DC∥AB,
∴△DQC∽△BQF,
∴
=
,
∵DC=AB=2,QF=2CQ,
∴BF=2DC=4,
∴AF=4-2=2,
在Rt△QAF中,由勾股定理得:QF2=AQ2+AF2,
∴(2CQ)2=CQ2+22,
∴CQ=
,
即AQ=CQ=
,
在Rt△QAB中,BQ=
=
=
.
∴DC=AD,∠CDQ=∠ADQ,
在△CDQ和△ADQ中
|
∴△CDQ≌△ADQ(SAS),
∴∠QAD=∠QCD;
(2)解:∵四边形ABCD是菱形,
∴DC=AB=2,DC∥AB,
∴△DQC∽△BQF,
∴
| DC |
| BF |
| CQ |
| QF |
∵DC=AB=2,QF=2CQ,
∴BF=2DC=4,
∴AF=4-2=2,
在Rt△QAF中,由勾股定理得:QF2=AQ2+AF2,
∴(2CQ)2=CQ2+22,
∴CQ=
2
| ||
| 3 |
即AQ=CQ=
2
| ||
| 3 |
在Rt△QAB中,BQ=
| AQ2+AB2 |
(
|
4
| ||
| 3 |
点评:本题考查了菱形的性质,全等三角形的性质和判定,相似三角形的性质和判定,勾股定理的应用,求出△CDQ≌△ADQ和得出关于CQ的方程是解此题的关键.

练习册系列答案
相关题目
下列图形:①三角形,②线段,③正方形,④直角,⑤平行四边形,其中一定是轴对称图形的个数是( )
| A、2个 | B、3个 | C、4个 | D、5个 |
下列各数中是无理数的是( )
| A、1.232232223 | |||
B、
| |||
C、
| |||
D、
|
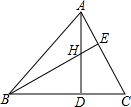 如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC的度数.
如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC的度数.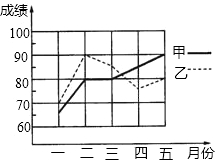 为了从甲、乙两名学生中选拔一人代表我校参加今年年底的全区中学生数学竞赛,统计了他们从今年1到5月的每个月的一次测验成绩(单位:分),如图是两人赛前5次测验成绩的折线统计图.
为了从甲、乙两名学生中选拔一人代表我校参加今年年底的全区中学生数学竞赛,统计了他们从今年1到5月的每个月的一次测验成绩(单位:分),如图是两人赛前5次测验成绩的折线统计图.