题目内容
10.方程2x+3y=11的正整数解有( )| A. | 无数个 | B. | 2个 | C. | 1个 | D. | 3个 |
分析 可把方程化y=$\frac{11-2x}{3}$,则可知11-2x为3的倍数且为正整数数,再取x为正整数代入讨论即可.
解答 解:方程可化为y=$\frac{11-2x}{3}$,
∵x、y为正整数,
∴11-2x为3的倍数且为正整数,
当x=1时,11-2x=11-2=9,此时y=3,
当x=2时,11-2x=7,不符合题意,
当x=3时,11-2x=11-6=5,不符合题意,
当x=4时,11-2x=11-8=3,此时y=1,
当x=5时,11-2x=11-10=1,不符合题意,
当x=6时,11-2x<0,不符合题意,
综上可知,方程的整数解为$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$、$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$共两个,
故选B.
点评 本题主要考查二元一次方程的特殊解,用含x的代数式表示出y,得出11-2x是3的倍数是解题的关键.

练习册系列答案
相关题目
1.若关于x的方程$\frac{x-2}{x+1}$=$\frac{m}{x+1}$产生增根,则常数m的值( )
| A. | -2 | B. | -1 | C. | -3 | D. | 2 |
18.下列方程中,是二元一次方程的有( )
①$\frac{5}{m}$-2n=12 ②$\frac{7}{4}$y-$\frac{11}{6}$z=-a ③$\frac{2}{a+b}$-1=3 ④mn+m=7 ⑤x+y=6.
①$\frac{5}{m}$-2n=12 ②$\frac{7}{4}$y-$\frac{11}{6}$z=-a ③$\frac{2}{a+b}$-1=3 ④mn+m=7 ⑤x+y=6.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.为保护生态环境,某县响应国家“退耕还林”号召,将某一部分耕地改为林地,改变后,林地面积和耕地面积共有180平方千米,耕地面积是林地面积的25%,为求改变后林地面积和耕地面积各多少平方千米.设改变后耕地面积x平方千米,林地地面积y平方千米,根据题意,列出如下四个方程组,其中正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=180}\\{x=y•25%}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=180}\\{y=x•25%}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=180}\\{x-y=25%}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=180}\\{y-x=25%}\end{array}\right.$ |
2.若正方形的对角线长为2,则这个正方形的面积为( )
| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
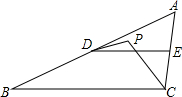 如图,在△ABC中,∠A=50°,DE∥BC,若PC平分∠ACB,DP平分∠ADE,则∠DPC=115°.
如图,在△ABC中,∠A=50°,DE∥BC,若PC平分∠ACB,DP平分∠ADE,则∠DPC=115°. 如图,过△ABC的边BC的中点M作直线垂直于∠A的平分线AA′,且分别交直线AB,AC于点E,F,求证:BE=CF=$\frac{1}{2}$(AB-AC).
如图,过△ABC的边BC的中点M作直线垂直于∠A的平分线AA′,且分别交直线AB,AC于点E,F,求证:BE=CF=$\frac{1}{2}$(AB-AC).