题目内容
2．若正方形的对角线长为2，则这个正方形的面积为（ ）| A． | 2 | B． | 4 | C． | $\sqrt{2}$ | D． | 2$\sqrt{2}$ |
分析 根据正方形的性质，对角线平分、相等、垂直且平分每一组对角求解即可．
解答 
解：∵四边形ABCD是正方形，
∴AO=BO=$\frac{1}{2}$AC=1cm，∠AOB=90°，
由勾股定理得，AB=$\sqrt{2}$cm，
S正=（$\sqrt{2}$）2=2cm2．
故选A．
点评 考查正方形的性质，关键是根据对角线平分、相等、垂直且平分每一组对角分析解答．
练习册系列答案
名校课堂系列答案
相关题目
13．已知关于x的一元二次方程x2+（2m-3）x+m2=0的两个不相等的实数根α，β满足$\frac{1}{α}$+$\frac{1}{β}$=1，则m的值为（ ）
| A． | -3 | B． | 1 | C． | -3 或1 | D． | 2 |
10．方程2x+3y=11的正整数解有（ ）
| A． | 无数个 | B． | 2个 | C． | 1个 | D． | 3个 |
如图，△ABD与△ACE均为正三角形，且AB＜AC，求证：BE=CD．
7．将方程组$\left\{\begin{array}{l}{8x-3y=9}\\{8x+4y=-5}\end{array}\right.$消去未知数x后得到的方程是（ ）
| A． | y=4 | B． | 7y=4 | C． | -7y=4 | D． | -7y=14 |
14．
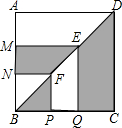如图，正方形ABCD的边长为x，点E、F分别是对角线BD上的两点，过点E、F作AD、AB的平行线，则图中阴影部分的面积的和为（ ）
如图，正方形ABCD的边长为x，点E、F分别是对角线BD上的两点，过点E、F作AD、AB的平行线，则图中阴影部分的面积的和为（ ）| A． | $\frac{1}{4}$x2 | B． | $\frac{1}{2}$x2 | C． | $\frac{1}{5}$x2 | D． | $\frac{1}{3}$x2 |
11．已知方程x2-5x-3=0的两个根分别为x1、x2，则x1+x2+x1x2的值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{\sqrt{15}}{4}$ | C． | -8 | D． | 2 |
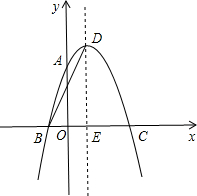如图，抛物线y=ax2+2x+c经过点A（0，3），B（-1，0），请解答下列问题：