题目内容
6.开口向上的抛物线y=a(x+2)(x-8)与x轴交于A,B两点,与y轴交于C点,若∠ACB=90°,则a的值是$\frac{1}{4}$.分析 求出抛物线y=a(x+2)(x-8)与x轴、y轴交点坐标,根据勾股定理列方程即可求出a的值.
解答 解:∵抛物线y=a(x+2)(x-8)与x轴交于A,B两点,与y轴交于C点,
∴A(-2,0)、B(8,0)、C(0,-16a)
∵∠ACB=90°,
∴AC2+BC2=AB2,
∴22+(16a)2+82+(16a)2=102,
解得:a=±$\frac{1}{4}$,
∵开口向上,
∴a=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题主要考查了抛物线与坐标轴的交点和勾股定理,熟练地运用数形结合思想是解决问题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
16.下列运算中错误的是( )
| A. | $\frac{a}{b}$=$\frac{a{c}^{2}}{b{c}^{2}}$ | B. | $\frac{-a-b}{a+b}$=-1 | ||
| C. | $\frac{0.5a+b}{0.2a-0.3b}$=$\frac{5a+10b}{2a-3b}$ | D. | $\frac{a}{b}$=$\frac{a({k}^{2}+1)}{b({k}^{2}+1)}$ |
11.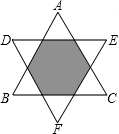 如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
 如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )
如图将正△ABC绕其中心至少旋转下列哪个角度才能得到另一个三角形( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
15.若9x2-kxy+49y2是一个完全平方式,那么k的值是( )
| A. | 42 | B. | -42 | C. | ±21 | D. | ±42 |
 如图,在长为10cm,宽为6cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是$\frac{108}{5}$cm2.
如图,在长为10cm,宽为6cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是$\frac{108}{5}$cm2.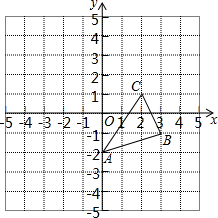 如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,-2),B(3,-1),C(2,1).
如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,-2),B(3,-1),C(2,1).