题目内容
2. 如图,在△ABC中,AD⊥BC于点D,若AB=3,BD=2,CD=1,则AC的长为( )
如图,在△ABC中,AD⊥BC于点D,若AB=3,BD=2,CD=1,则AC的长为( )| A. | 6 | B. | $\sqrt{6}$ | C. | $\sqrt{5}$ | D. | 4 |
分析 由勾股定理先求出Rt△ADB的直角边AD的长,然后再根据勾股定理求Rt△ADC的斜边AC的长即可.
解答 解:如图,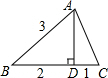
∵在△ABC中,AD⊥BC于点D,
∴∠ADB=∠ADC=90°.
∵在Rt△ADB中,AB=3,BD=2,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$
在Rt△ADC中,AD=$\sqrt{5}$,CD=1,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{(\sqrt{5})^{2}+{1}^{2}}$=$\sqrt{6}$
故:选B
点评 本题考查了勾股定理的应用,解题的关键是理解勾股定理.

练习册系列答案
相关题目
12.下列各组数中,不能满足勾股定理的逆定理是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 5,12,13 | D. | 7,5,10 |
13.当a,b互为相反数时,代数式a2+ab-2的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | -1 |
10. 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,如果四边形ABCD的面积为8,那么BE的长为( )
如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,如果四边形ABCD的面积为8,那么BE的长为( )
 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,如果四边形ABCD的面积为8,那么BE的长为( )
如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,如果四边形ABCD的面积为8,那么BE的长为( )| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
17. 如图,在四边形ABCD中,点E,F,G分别是边AB,AD,DC的中点,则EF=( )
如图,在四边形ABCD中,点E,F,G分别是边AB,AD,DC的中点,则EF=( )
 如图,在四边形ABCD中,点E,F,G分别是边AB,AD,DC的中点,则EF=( )
如图,在四边形ABCD中,点E,F,G分别是边AB,AD,DC的中点,则EF=( )| A. | $\frac{1}{3}$BD | B. | $\frac{1}{2}$BD | C. | $\frac{1}{2}$BG | D. | BG |
11.函数y=x|x|-3x+1的图象与x轴交点的个数为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 0 |
12. 如图,已知△ABC与△DEF分别是等边三角形和等腰直角三角形,AC与DF交于点G,AD与FC分别是△ABC和△DEF的高,线段BC,DE在同一条直线上,则下列说法不正确的是( )
如图,已知△ABC与△DEF分别是等边三角形和等腰直角三角形,AC与DF交于点G,AD与FC分别是△ABC和△DEF的高,线段BC,DE在同一条直线上,则下列说法不正确的是( )
 如图,已知△ABC与△DEF分别是等边三角形和等腰直角三角形,AC与DF交于点G,AD与FC分别是△ABC和△DEF的高,线段BC,DE在同一条直线上,则下列说法不正确的是( )
如图,已知△ABC与△DEF分别是等边三角形和等腰直角三角形,AC与DF交于点G,AD与FC分别是△ABC和△DEF的高,线段BC,DE在同一条直线上,则下列说法不正确的是( )| A. | △AGD∽△CGF | B. | △AGD∽△DGC | C. | $\frac{{S}_{△AGD}}{{S}_{△CGF}}$=3 | D. | $\frac{AG}{CG}$=$\sqrt{3}$ |
 将两块全等的三角板如图放置,点O为AB中点,AB=A′B′=10,BC=B′C′=6,现将三角板A′B′C′绕点O旋转,B′C′、A′B′与边AC分别交于点M、N,当CM=$\frac{25}{8}$或$\frac{7}{4}$时,△OMN与△BCO相似.
将两块全等的三角板如图放置,点O为AB中点,AB=A′B′=10,BC=B′C′=6,现将三角板A′B′C′绕点O旋转,B′C′、A′B′与边AC分别交于点M、N,当CM=$\frac{25}{8}$或$\frac{7}{4}$时,△OMN与△BCO相似.