题目内容
7.已知菱形ABCD中,∠ABC=60°,点O是对角线AC的中点,点P为直线AC上一点,M为BC延长线上一点,且CM=AP.(1)如图1.当点P在OC上(不与O,C重合)移动时,
①求证:PD=PM;
②∠DPM的度数是否发生变化?试证明你的结论;
(2)如图2,当点P在OC的延长线上时,(1)中的两个结论是否仍然成立?请自己画图证明.

分析 (1)①先根据菱形的性质得出AD=CD,∠DAP=∠DCP=60°,再由SAS定理得出△APD≌△CMD,故可得出PD=DM,∠ADP=∠CDM,△DPM是等边三角形,由此可得出结论;
②根据①中,△DPM是等边三角形可得出结论.
(2)连接DP,MP,同(1)可得△APD≌△CMD,故可得出PD=DM,∠ADP=∠CDM,△DPM是等边三角形,由等边三角形的性质即可得出结论.
解答 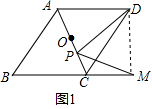 (1)①证明:∵菱形ABCD中,∠ABC=60°,
(1)①证明:∵菱形ABCD中,∠ABC=60°,
∴AD=CD,∠DAP=∠DCP=60°,
在△APD和△CMD中,
$\left\{\begin{array}{l}AD=CD\\∠DAP=∠DCP\\ AP=CM\end{array}\right.$,
∴△APD≌△CMD(SAS).
∴PD=DM,∠ADP=∠CDM,
∴∠PDM=∠PDC+∠CDM=∠PDC+∠ADP=∠ADC=60°,
∴△DPM是等边三角形,
∴PD=PM.
②不变.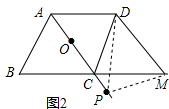
证明:∵由①知△DPM是等边三角形,
∴∠DPM=60°,且与点P位置无关;
(2)成立.
连接DP,MP,同(1)可得△APD≌△CMD,
∴PD=DM,∠ADP=∠CDM,△DPM是等边三角形,
∴PD=PM,∠DPM=60°.
点评 本题考查的是菱形的性质,根据题意,作出辅助线,构造出等边三角形是解答此题的关键.

练习册系列答案
相关题目
19.已知一次函数y=kx+b中,y随自变量x的增大而增大,则有( )
| A. | b<0 | B. | b>0 | C. | k<0 | D. | k>0 |
16. 如图,△ABC与△AED是全等三角形,即△ABC≌△AED,那么图中相等的角有( )
如图,△ABC与△AED是全等三角形,即△ABC≌△AED,那么图中相等的角有( )
 如图,△ABC与△AED是全等三角形,即△ABC≌△AED,那么图中相等的角有( )
如图,△ABC与△AED是全等三角形,即△ABC≌△AED,那么图中相等的角有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
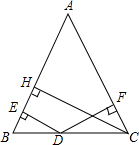 已知:如图所示,△ABC中,AB=AC,D是BC上任意一点,DE⊥AB于E,DF⊥AC于F,CH⊥AB于H,DE=2,DF=6,则CH=8.
已知:如图所示,△ABC中,AB=AC,D是BC上任意一点,DE⊥AB于E,DF⊥AC于F,CH⊥AB于H,DE=2,DF=6,则CH=8. 如图,长方形ABCD沿AE折叠,使点B落在CD边上的点F处,如果∠EFC=70°,那么∠BAE=10°.
如图,长方形ABCD沿AE折叠,使点B落在CD边上的点F处,如果∠EFC=70°,那么∠BAE=10°.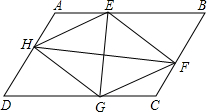 如图,在?ABCD中,AE=CG,BF=DH,求证:EG与HF互相平分.
如图,在?ABCD中,AE=CG,BF=DH,求证:EG与HF互相平分.