题目内容
1.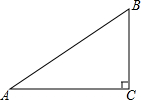 如图,在Rt△ABC中,∠C=90°,∠B=60°,AC=8,求AB的长.
如图,在Rt△ABC中,∠C=90°,∠B=60°,AC=8,求AB的长.
分析 由条件可求得∠A=30°,设BC=x,则AB=2x,由勾股定理可列方程,可求得x的值,则可求得AB的长.
解答 解:
∵在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°,
∴设BC=x,则AB=2x,
∵AC2+BC2=AB2,
∴82+x2=(2x)2,解得x=$\frac{8\sqrt{3}}{3}$或x=-$\frac{8\sqrt{3}}{3}$(舍去),
∴AB=2x=$\frac{16\sqrt{3}}{3}$.
点评 本题主要考查直角三角形的性质,掌握在直角三角形中,30°所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
相关题目
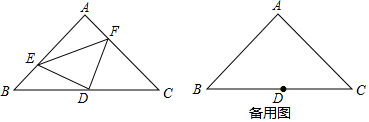
 如图,△ABC中,AB=AC,PB=PC,连接AP并延长交BC于D,求证:AD垂直平分BC.
如图,△ABC中,AB=AC,PB=PC,连接AP并延长交BC于D,求证:AD垂直平分BC.
 (1)根据作图要求(尺规作图,保留作图痕迹,不写作法).
(1)根据作图要求(尺规作图,保留作图痕迹,不写作法).