题目内容
10. 已知:△ABC内接于⊙O,AD是高,E是BC中点,求证:AE平分∠OAD.
已知:△ABC内接于⊙O,AD是高,E是BC中点,求证:AE平分∠OAD.
分析 连接OE,由垂径定理得出OE⊥BC,证出OE∥AD,由平行线的性质得出∠OEA=∠DAE,再由等腰三角形的性质得出∠OAE=∠DAE,即可得出结论.
解答 证明: 连接OE,如图所示:
连接OE,如图所示:
∵E是$\widehat{BC}$的中点,
∴OE⊥BC,
∵AD是高,
∴AD⊥BC,
∴OE∥AD,
∴∠OEA=∠DAE,
∵OA=OE,
∴∠OEA=∠OAE,
∴∠OAE=∠DAE,
即AE平分∠OAD.
点评 本题考查了三角形的外接圆与外心、垂径定理、平行线的判定与性质、等腰三角形的性质;熟练掌握垂径定理,证出OE∥AD是解决问题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
20. 如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
 如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )| A. | $\frac{12}{5}$ | B. | $\frac{14}{5}$ | C. | $\frac{16}{5}$ | D. | 4 |
1.分式$\frac{x}{x-1}$+$\frac{1}{1-x}$可化简为( )
| A. | $\frac{x+1}{x-1}$ | B. | 1 | C. | -1 | D. | $\frac{x+1}{1-x}$ |
15.如果单项式-xa+1y3与12ybx2是同类项,那么a、b的值分别为( )
| A. | 1,1? | B. | 2,3 | C. | 1,3? | D. | 2,1 |
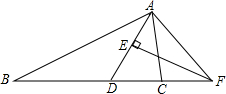 如图,在△ABC中,AD平分∠BAC,EF垂直平分AD交BC的延长线于点F,判断∠CAF与∠B的大小关系,并说明理由.
如图,在△ABC中,AD平分∠BAC,EF垂直平分AD交BC的延长线于点F,判断∠CAF与∠B的大小关系,并说明理由.