题目内容
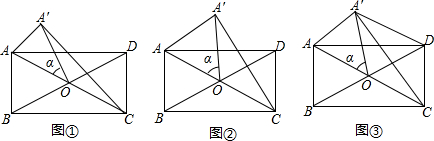
19.在矩形ABCD中,AB=1,BC=2,对角线AC、BD相交于点O,点A绕点O按顺时针方向旋转到A′,旋转角为α(0°<α<∠AOD),连接A′C.(1)如图①,则△AA′C的形状是直角三角形;
(2)如图②,当∠α=60°,求A′C长度;
(3)如图③,当∠α=∠AOB时,求证:A′D∥AC.
分析 (1)根据矩形的性质和旋转的性质求得OA=OB=OC=OD=OA′,然后根据等腰三角形的性质得出∠OAA′=∠OA′A,∠OA′C=∠OCA′,进而得出∠CA′A=90°;
(2)根据勾股定理求得AC,然后求得△AA′O是等边三角形,解直角三角形A′AC即可求得A′C长度;
(3)根据旋转的性质和矩形的性质求得∠OAA′=∠OCD,AA′=CD,证得四边形A′ACD是等腰梯形,从而证得A′D∥AC.
解答 解:(1)∵四边形ABCD是矩形,
∴OA=OB=OC=OD,
∵OA=OA′,
∴OA′=OC,
∴∠OAA′=∠OA′A,∠OA′C=∠OCA′,
∴∠OA′C+∠OA′A=∠OCA′+∠OAA′,
∴∠CA′A=90°,
∴△AA′C是直角三角形,
故答案为:直角三角形;
(2)∵AB=1,BC=2,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{5}$,
∴OA=OA′=$\frac{\sqrt{5}}{2}$,
∵∠α=60°,
∴△AA′O是等边三角形,
∴∠OAA′=60°,
∴A′C=$\frac{\sqrt{3}}{2}$AC=$\frac{\sqrt{3}}{2}$×$\sqrt{5}$=$\frac{\sqrt{15}}{2}$;
(3)∵∠α=∠AOB,OA=OB=OA′,
∴AA′=AB,∠OAA′=∠OBA,
∵四边形ABCD是矩形,
∴∠OBA=∠OCD,AB=CD,
∴∠OAA′=∠OCD,AA′=CD,
∴四边形A′ACD是等腰梯形,
∴A′D∥AC.
点评 本题考查了矩形的性质,旋转的性质,等腰三角形的判定和性质,勾股定理的应用等,熟练运用旋转的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
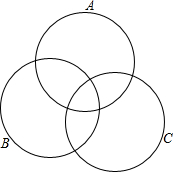 已知A、B、C三个数集,每一个数集中所包含的数都写在各自的大括号内,请把这些数填在图圈内相应的位置.
已知A、B、C三个数集,每一个数集中所包含的数都写在各自的大括号内,请把这些数填在图圈内相应的位置.