题目内容
11.甲乙两人骑自行车同时从A地出发去B地,甲的车速是乙的车速的1.2倍,乙骑了5千米后,自行车出现故障,耽误的时间可以骑全程的$\frac{1}{6}$.排除故障后,乙的速度提高了60%,结果甲乙同时到达B地,那么A,B两地之间的距离为45千米.分析 根据题意可知,甲乙的车速比是1.2:1=6:5,所以所用时间比为5:6,不妨设甲用时5t,则乙原定时间为6t,乙因故障耽误的时间为 $\frac{1}{6}$×6t=t,而最后全程用时5t,所以故障排除后,乙的提速使它节省了2t的时间.提速后的速度与原来速度比为1.6:1=8:5,所以时间比为5:8,节省了三份的时间,所以每份为 t,所以这段路原计划用时$\frac{2}{3}$t×8=$\frac{16}{3}$t,所以一开始的5千米原计划用时是6t-$\frac{16}{3}$t=$\frac{2}{3}$t,所以A、B之间的距离为5×(6t÷$\frac{2}{3}$t),然后计算即可.
解答 解:甲乙的车速比是1.2:1=6:5,所以所用时间比为5:6;设甲用时5t,则乙原定时间为6t;
乙因故障耽误的时间为 $\frac{1}{6}$×6t=t,而最后全程用时5t,所以故障排除后,乙的提速使它节省了2t的时间.
提速后的速度与原来速度比为1.6:1=8:5,所以时间比为5:8,节省了三份的时间,所以每份为 t,
所以这段路原计划用时$\frac{2}{3}$t×8=$\frac{16}{3}$t,所以一开始的5千米原计划用时是6t-$\frac{16}{3}$t=$\frac{2}{3}$t,
所以A、B之间的距离为:
5×(6t÷t),
=5×9,
=45(千米);
故答案为:45.
点评 此题主要考查了分式方程的应用,关键是根据甲乙的车速比,求出甲乙的时间之比,然后根据时间之间的关系,求出一开始的5千米原计划用时,最后求出A、B之间的距离.

练习册系列答案
相关题目
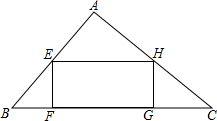 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,四边形EFGH为△ABC的内接矩形,设EF=x,EH=y.
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,四边形EFGH为△ABC的内接矩形,设EF=x,EH=y. 如图,在?ABCD中,∠ABC的平分线交AD于点E,且点E把AD分成5cm与4cm的两部分,求?ABCD的周长.
如图,在?ABCD中,∠ABC的平分线交AD于点E,且点E把AD分成5cm与4cm的两部分,求?ABCD的周长. 已知:b是最小的正整数,且a、b满足(c-5)2+|a+b|=0,请回答问题:
已知:b是最小的正整数,且a、b满足(c-5)2+|a+b|=0,请回答问题: