题目内容
工人师傅对如图所示的零件进行加工，把材料弯成了一个40°的锐角，然后准备在A处第二次加工拐弯，要保证弯过来的部分与BC保持平行，弯的角度是（ ）| A、40° | B、140° |
| C、40°或140° | D、50° |
考点：平行线的判定
专题：应用题
分析：需要分类讨论：从点A处向左边弯和从点A处想右边弯两种情况．
解答：
解：如图1，作AE∥BC，
则∠CBA=∠EAB=40°；
如图2，作AE∥BC，
则∠CBA+∠EAB=180°，
∵∠CBA=40°，
∴∠EAB=140°，
综上所述，弯的角度是40°或140°．
故选：C．
解：如图1，作AE∥BC，则∠CBA=∠EAB=40°；
如图2，作AE∥BC，
则∠CBA+∠EAB=180°，
∵∠CBA=40°，
∴∠EAB=140°，
综上所述，弯的角度是40°或140°．
故选：C．
点评：本题考查了平行线的性质的应用，注意：两直线平行，同旁内角互补．
练习册系列答案
小学能力测试卷系列答案
相关题目
用配方法将一元二次方程x2-6x-4=0变形为（x+m）2=n的形式是（ ）
| A、（x+3）2=13 |
| B、（x-3）2=4 |
| C、（x-3）2=5 |
| D、（x-3）2=13 |
下列命题中真命题是（ ）
①内错角相等；
②如果a+b=0，那么
=
；
③邻补角互补；
④相等的角是对顶角；
⑤如果a+b=0，那么
=
．
①内错角相等；
②如果a+b=0，那么
| 3 | a |
| 3 | -b |
③邻补角互补；
④相等的角是对顶角；
⑤如果a+b=0，那么
| a2 |
| b2 |
| A、①②③④⑤ | B、②③④⑤ |
| C、②③⑤ | D、①④⑤ |
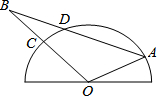如图，半圆O是一个量角器，△AOB为一纸片，AB交半圆于点D，OB交半圆于点C，若点C、D、A在量角器上对应读数分别为45°，70°，160°，则∠B的度数为（ ）| A、20° | B、30° |
| C、45° | D、60° |
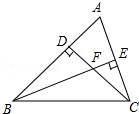已知：如图，△ABC中，∠ABC=45°，AC=4cm，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点F．则BF=（ ）| A、4cm | B、3cm |
| C、2cm | D、1cm |
若
=
，则
=（ ）
| a |
| b |
| 3 |
| 4 |
| a+b |
| b |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
如图，已知∠B=∠EFD，BF=CE，添加下列一个条件，不能使△ABC≌△DEF的是（ ）| A、∠A=∠D |
| B、∠ACB=∠E |
| C、AB=DF |
| D、AC=DE |
已知△ABC中，∠A=2∠B=3∠C，则△ABC为（ ）
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、无法确定 |
如图，等腰梯形ABCD是一个四棱柱的俯视图，它的高为5，AD=3，AE⊥BC于点E，AE=4，BC=7，求此四棱柱的三种视图的面积和．