题目内容
用配方法将一元二次方程x2-6x-4=0变形为（x+m）2=n的形式是（ ）
| A、（x+3）2=13 |
| B、（x-3）2=4 |
| C、（x-3）2=5 |
| D、（x-3）2=13 |
考点：解一元二次方程-配方法
专题：计算题,配方法
分析：先移项，然后两边同时加上一次项系数一半的平方．
解答：解：x2-6x-4=0，
移项得，x2-6x=4，
配方得，x2-6x+32=4+32，
（x-3）2=13，
故选D．
移项得，x2-6x=4，
配方得，x2-6x+32=4+32，
（x-3）2=13，
故选D．
点评：本题考查了解一元二次方程--配方法，配方法的一般步骤：
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
练习册系列答案
相关题目
下列计算正确的个数是（ ）
①a5•a5=a10；②b5+b5=b10；③x5•x5=x25；④y5•y5=2y10；⑤c•c3=c3；⑥m•m3=m4；⑦（-x）•（-x）2=-x3；⑧y•y2•y4=y7．
①a5•a5=a10；②b5+b5=b10；③x5•x5=x25；④y5•y5=2y10；⑤c•c3=c3；⑥m•m3=m4；⑦（-x）•（-x）2=-x3；⑧y•y2•y4=y7．
| A、2 | B、3 | C、4 | D、5 |
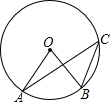如图，已知⊙O的圆心角∠AOB=80°，则圆周角∠ACB的度数等于（ ）| A、160° | B、100° |
| C、80° | D、40° |
下列各式
，
，
x2y，-
，
，
中，是分式的有（ ）
| 2 |
| x |
| x+1 |
| x |
| 1 |
| 2 |
| a2b2 |
| 4 |
| 1 |
| a+5 |
| m+a |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知一次函数y=kx-k，若y随x的减小而减小，则该函数的图象经过第（ ） 象限．
| A、一、二、三 |
| B、一、二、四 |
| C、一、三、四 |
| D、二、三、四 |
下列命题不正确的是（ ）
| A、角平分钱上的点到角两边的距离相等 |
| B、两边对应成比等且有一个角对应相等的两个三角形相似 |
| C、位似的两个图形一定相似 |
| D、三角函数值的大小与角两边的长短无关 |
工人师傅对如图所示的零件进行加工，把材料弯成了一个40°的锐角，然后准备在A处第二次加工拐弯，要保证弯过来的部分与BC保持平行，弯的角度是（ ）| A、40° | B、140° |
| C、40°或140° | D、50° |