题目内容
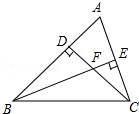 已知:如图,△ABC中,∠ABC=45°,AC=4cm,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点F.则BF=( )
已知:如图,△ABC中,∠ABC=45°,AC=4cm,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点F.则BF=( )| A、4cm | B、3cm |
| C、2cm | D、1cm |
考点:全等三角形的判定与性质
专题:
分析:求出∠BDF=∠CDA,BD=DC,∠DBF=∠ACD,证△BDF≌△CDA,推出BF=AC即可.
解答:解:∵CD⊥AB,BE⊥AC,
∴∠BDC=∠CDA=∠AEB=90°,
∴∠ABF=∠ACD=90°-∠A,
∵∠ABC=45°,
∴∠DCB=45°=∠ABC,
∴BD=DC,
在△BDF和△CDA中
∴△BDF≌△CDA,
∴BF=AC=4cm,
故选A.
∴∠BDC=∠CDA=∠AEB=90°,
∴∠ABF=∠ACD=90°-∠A,
∵∠ABC=45°,
∴∠DCB=45°=∠ABC,
∴BD=DC,
在△BDF和△CDA中
|
∴△BDF≌△CDA,
∴BF=AC=4cm,
故选A.
点评:本题考查了全等三角形的性质和判定的应用,关键是推出△BDF≌△CDA,主要考查学生的推理能力.

练习册系列答案
相关题目
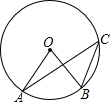 如图,已知⊙O的圆心角∠AOB=80°,则圆周角∠ACB的度数等于( )
如图,已知⊙O的圆心角∠AOB=80°,则圆周角∠ACB的度数等于( )| A、160° | B、100° |
| C、80° | D、40° |
钟面角是指时钟的时针与分针所成的角.当时间是9:30时,钟面角等于( )
| A、90° | B、102° |
| C、105° | D、120° |
如果把分式
中的x和y都扩大2倍,那么分式的值( )
| x+y |
| 2xy |
| A、不变 | B、扩大2倍 |
| C、扩大4倍 | D、缩小2倍 |
2012年4月13日国家统计局举行发布会,一季度全国城镇新增工作岗位332万个,332万个可用科学记数法表示为( )
| A、3.32×105个 |
| B、3.32×106个 |
| C、33.2×105个 |
| D、0.332×107个 |
 工人师傅对如图所示的零件进行加工,把材料弯成了一个40°的锐角,然后准备在A处第二次加工拐弯,要保证弯过来的部分与BC保持平行,弯的角度是( )
工人师傅对如图所示的零件进行加工,把材料弯成了一个40°的锐角,然后准备在A处第二次加工拐弯,要保证弯过来的部分与BC保持平行,弯的角度是( )| A、40° | B、140° |
| C、40°或140° | D、50° |
已知a≠0,下列计算正确的是( )
| A、a2+a3=a5 |
| B、a2•a3=a6 |
| C、a3÷a2=a |
| D、(a2)3=a5 |
 如图,△ABC中,∠C=60°,剪去这个60°角后,得到一个四边形,那么∠BDE+∠AED的度数为( )
如图,△ABC中,∠C=60°,剪去这个60°角后,得到一个四边形,那么∠BDE+∠AED的度数为( )| A、180° | B、240° |
| C、120° | D、300° |