题目内容
10．
如图，△ABC为⊙O的内接三角形，∠BOC=80°，则∠A等于（ ）| A． | 80 | B． | 60 | C． | 50 | D． | 40 |
分析 根据圆周角定理计算即可．
解答 解：由圆周角定理得，∠A=$\frac{1}{2}$∠BOC=40°，
故选：D．
点评 本题考查的是三角形的外接圆与外心的概念和性质，掌握圆周角定理是解题的关键．
练习册系列答案
天天练口算系列答案
相关题目
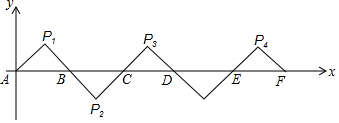
20．如图所示，在平面直角坐标系中A（0，0），B（2，0），△AP1B是等腰直角三角形，且∠P1=90°，把△AP1B绕点B顺时针旋转180°，得到△BP2C；把△BP2C绕点C顺时针旋转180°，得到△CP3D，依此类推，则旋转第2016次后，得到的等腰直角三角形的直角顶点P2017的坐标为（ ）
| A． | （4030，1） | B． | （4029，-1） | C． | （4033，1） | D． | （4031，-1） |
1．下列关于矩形的说法，正确的是（ ）
| A． | 对角线相等的四边形是矩形 | B． | 对角线互相平分的四边形是矩形 | ||
| C． | 矩形的对角线相等且互相平分 | D． | 矩形的对角线互相垂直且平分 |
18．下列三条线段不能构成三角形的三边的是（ ）
| A． | 3cm，4cm，5cm | B． | 5cm，6cm，11cm | C． | 5cm，6cm，10cm | D． | 2cm，3cm，4cm |
5．
如图，AB是⊙O的直径，C、D是⊙O上的点，∠CDB=30°，过点C作⊙O的切线交AB的延长线于点E，则sin∠E的值是（ ）
如图，AB是⊙O的直径，C、D是⊙O上的点，∠CDB=30°，过点C作⊙O的切线交AB的延长线于点E，则sin∠E的值是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | $\frac{\sqrt{3}}{2}$ |
15．下列说法中，正确的是（ ）
| A． | 有一个角是直角的四边形是菱形 | |
| B． | 对角线互相垂直的菱形是正方形 | |
| C． | 对角线相等的平行四边形是矩形 | |
| D． | 一组邻边相等的平行四边形是正方形 |
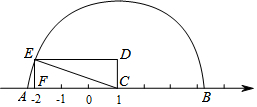如图所示，数轴上点C表示的数是1，点F表示的数是-2，CD=1，以CD，CF为边作长方形CDEF，以C为圆心、CE的长为半径画弧交数轴于A、B两点，则点A表示的数是1-$\sqrt{10}$，点B表示的数是1+$\sqrt{10}$．