题目内容
20.如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,则旋转第2016次后,得到的等腰直角三角形的直角顶点P2017的坐标为( )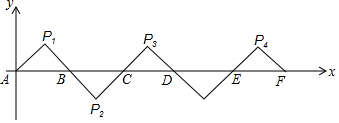
| A. | (4030,1) | B. | (4029,-1) | C. | (4033,1) | D. | (4031,-1) |
分析 作P1⊥x轴于H,利用等腰直角三角形的性质得P1H=$\frac{1}{2}$AB=1,AH=BH=1,则P1的纵坐标为1,再利用旋转的性质易得P2的纵坐标为-1,P3的纵坐标为1,P4的纵坐标为-1,P5的纵坐标为1,…,于是可判断P1017的纵坐标为1,而横坐标为2017×2-1=4033,所以P1017(4033,1).
解答 解:作P1⊥x轴于H,
∵A(0,0),B(2,0),
∴AB=2,
∵△AP1B是等腰直角三角形,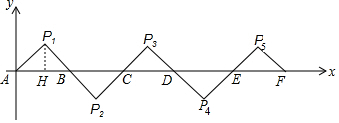
∴P1H=$\frac{1}{2}$AB=1,AH=BH=1,
∴P1的纵坐标为1,
∵△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D,
∴P2的纵坐标为-1,P3的纵坐标为1,P4的纵坐标为-1,P5的纵坐标为1,…,
∴P1017的纵坐标为1,横坐标为2017×2-1=4033,
即P1017(4033,1).
故选C.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.也考查了等腰直角三角形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图所示,直线a、b被直线c所截,∠1与∠2是( )
如图所示,直线a、b被直线c所截,∠1与∠2是( )
 如图所示,直线a、b被直线c所截,∠1与∠2是( )
如图所示,直线a、b被直线c所截,∠1与∠2是( )| A. | 内错角 | B. | 同位角 | C. | 同旁内角 | D. | 邻补角 |
8.在函数y=$\sqrt{x-2}$中,自变量x的取值范围是( )
| A. | x<2 | B. | x≤2 | C. | x>2 | D. | x≥2 |
5.一元二次方程x2+2x+2=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 只有一个实数根 |
12. 小红制作了一个正方体,其表面展开图如图所示,正方体中与“文”所对的面上的汉字应是( )
小红制作了一个正方体,其表面展开图如图所示,正方体中与“文”所对的面上的汉字应是( )
 小红制作了一个正方体,其表面展开图如图所示,正方体中与“文”所对的面上的汉字应是( )
小红制作了一个正方体,其表面展开图如图所示,正方体中与“文”所对的面上的汉字应是( )| A. | 城 | B. | 明 | C. | 全 | D. | 国 |
9.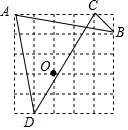 如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )
如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )
 如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )
如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )| A. | △ACD的外心 | B. | △ABC的外心 | C. | △ACD的内心 | D. | △ABC的内心 |
10. 如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )
如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )
 如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )
如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )| A. | 80 | B. | 60 | C. | 50 | D. | 40 |
 如图所示,正方形边长为2a,则阴影部分的面积y与a之间的函数关系式为(2π-4)a2.
如图所示,正方形边长为2a,则阴影部分的面积y与a之间的函数关系式为(2π-4)a2.