题目内容
5. 如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则sin∠E的值是( )
如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则sin∠E的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 连接OC,如图,利用圆周角定理得到∠BOC=∠CDB=30°,再根据切线的性质得∠OCE=90°,所以∠E=30°,然后根据特殊角的三角函数值求解.
解答 解:连接OC,如图,
∠BOC=∠CDB=30°,
∵CE为切线,
∴OC⊥CE,
∴∠OCE=90°,
∴∠E=30°,
∴sinE=sin30°=$\frac{1}{2}$.
故选A.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆周角定理和特殊角的三角函数值.

练习册系列答案
相关题目
16.把多项式x2+ax+b分解因式,得(x+1)(x-3),则a,b的值分别是( )
| A. | a=-2,b=-3 | B. | a=2,b=3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
13.关于x的一元二次方程 kx2+2x-1=0有两个不相等实数根,则k 的取值范围是( )
| A. | k>-1 | B. | k≥-1 | C. | k≠0 | D. | k>-1且k≠0 |
20.平行四边形、矩形、正方形之间的关系是( )
| A. |  | B. |  | C. |  | D. |  |
10. 如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )
如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )
 如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )
如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )| A. | 80 | B. | 60 | C. | 50 | D. | 40 |
15.用四舍五入法按要求对0.05019分别去近似值,其中错误的是( )
| A. | 0.1(精确到0.1) | B. | 0.05(精确到百分位) | ||
| C. | 0.0501(精确到0.0001) | D. | 0.0502(精确到0.0001) |
 如图,直线y=kx+b过A(-1,2),B(-2,0)两点,则0≤kx+b<4的解集为-2≤x<0.
如图,直线y=kx+b过A(-1,2),B(-2,0)两点,则0≤kx+b<4的解集为-2≤x<0.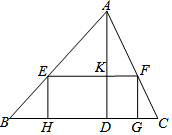 如图,已知锐角△ABC中,边BC长为12,高AD长为8.矩形EFGH的边GH在BC边长,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
如图,已知锐角△ABC中,边BC长为12,高AD长为8.矩形EFGH的边GH在BC边长,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.