题目内容
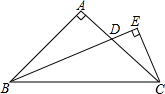 如图,在Rt△ABC中,AB=AC,∠BAC=90°,BD平分∠ABC交AC于点D,CE⊥BD交BD的延长线于点E,则线段BD和CE具有什么数量关系,并证明你的结论.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,BD平分∠ABC交AC于点D,CE⊥BD交BD的延长线于点E,则线段BD和CE具有什么数量关系,并证明你的结论.考点:全等三角形的判定与性质
专题:
分析:延长CE与BA延长线交于点F,首先证明△BAD≌△CAF,根据全等三角形的性质可得BD=CF,再证明△BEF≌△BCE可得CE=EF,进而可得BD=2CE.
解答: 答:BD=2CE,
答:BD=2CE,
延长CE与BA延长线交于点F,
∵∠BAC=90°,CE⊥BD,
∴∠BAC=∠DEC,
∵∠ADB=∠CDE,
∴∠ABD=∠DCE,
在△BAD和△CAF中,
,
∴△BAD≌△CAF(ASA),
∴BD=CF,
∵BD平分∠ABC,CE⊥DB,
∴∠FBE=∠CBE,
在△BEF和△BCE中,
,
∴△BEF≌△BCE(AAS),
∴CE=EF,
∴DB=2CE.
 答:BD=2CE,
答:BD=2CE,延长CE与BA延长线交于点F,
∵∠BAC=90°,CE⊥BD,
∴∠BAC=∠DEC,
∵∠ADB=∠CDE,
∴∠ABD=∠DCE,
在△BAD和△CAF中,
|
∴△BAD≌△CAF(ASA),
∴BD=CF,
∵BD平分∠ABC,CE⊥DB,
∴∠FBE=∠CBE,
在△BEF和△BCE中,
|
∴△BEF≌△BCE(AAS),
∴CE=EF,
∴DB=2CE.
点评:此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定方法,全等三角形对应边相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOD=70°,则∠BOD的大小为( )
如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOD=70°,则∠BOD的大小为( )| A、25° | B、35° |
| C、45° | D、55° |
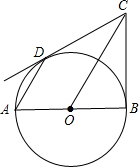 如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.
如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.(1)求证:DC是⊙O的切线;
(2)若OB=1,劣弧
 |
| BD |
下列叙述正确的是( )
| A、“13位同学中有两人出生的月份相同”是随机事件 |
| B、小亮掷硬币100次,其中44次正面朝上,则小亮掷硬币一次正面朝上的概率为0.44 |
| C、“明天降雨的概率是80%”,即明天下雨有80%的可能性 |
| D、彩票的中奖概率为1%,买100张才会中奖 |
 求阴影部分的周长.
求阴影部分的周长.
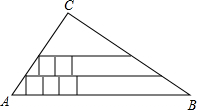 如图,在Rt△ABC中,∠C为直角,AC=6,BC=8.在Rt△ABC内从左往右叠放边长为1.2的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放
如图,在Rt△ABC中,∠C为直角,AC=6,BC=8.在Rt△ABC内从左往右叠放边长为1.2的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放