题目内容
有一个十进制的六位数
（其中a、b、c、d、e分别是这个六位数的万位、千位、百位、十位、个位上的数字）乘以3后，变成一个新的六位数
，则原来的六位数
是 ．
. |
| 1abcde |
. |
| abcde1 |
. |
| 1abcde |
考点：一元一次方程的应用
专题：数字问题
分析：设5位数abcde为y，这个六位数就可以表示为100000+y，乘以3后的结果是10y+1，根据数字问题的等量关系建立方程求出其解即可．
解答：解：设5位数abcde为y，由题意，得
3（100000+y）=10y+1，
解得y=42857．
则这个六位数为：142857．
答：这个六位数是142857．
故答案为：142857．
3（100000+y）=10y+1，
解得y=42857．
则这个六位数为：142857．
答：这个六位数是142857．
故答案为：142857．
点评：本题考查了数字问题的数量关系的运用，列一元一次方程解实际问题的运用，一元一次方程的解法的运用，解答时根据数字问题的数量关系建立方程是关键，
练习册系列答案
相关题目
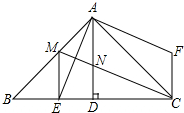如图，△ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足是D，AE平分∠BAD，交BC于点E．在△ABC外有一点F，使FA⊥AE，FC⊥BC．
如图点C是线段BD上一点，分别以BC和CD为一边，在BD的同侧作等边△ABC和等边△ECD，AC交BE于点G，CE交AD于点F．
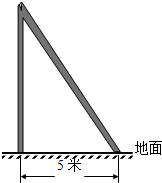如图，一木杆原来垂直于地面，在离地某处断裂，木杆顶部落在离木杆底部5米处，已知木杆原长25米，求木杆断裂处离地面多少米？
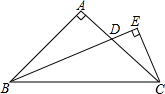如图，在Rt△ABC中，AB=AC，∠BAC=90°，BD平分∠ABC交AC于点D，CE⊥BD交BD的延长线于点E，则线段BD和CE具有什么数量关系，并证明你的结论．
如图，在矩形ABCD中，DE⊥AC于E，设∠ADE=a，且sinα=