Question

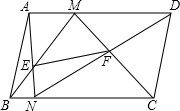如图所示，在平行四边形ABCD中，M，N分别在AD，BC上，AN和BM交于点E，CM和DN交于点F，连结EF．
（1）当M，N分别为AD，BC的中点时，试判断四边形MENF的形状，并说明理由；
（2）试探求：
①当AM，BN满足什么条件时，一定有EF

∥

.

1

2

AD？并说明理由；
②当AM，BN满足什么条件时，一定有四边形MENF为平行四边形？并说明理由．

Answer 1

考点：平行四边形的判定与性质,三角形中位线定理

专题：

分析：（1）根据平行四边形的对边相等可得AD=BC，然后求出AM=CN，再根据一组对边平行且相等的四边形是平行四边形证明得到四边形ANCM是平行四边形，根据平行四边形的对边平行可得AN∥CM，同理可得BM∥DN，再根据平行四边形的定义解答；
（2）①当AM=BN时，可得AE=EN，同理可得DF=FN，再根据三角形的中位线平行于第三边并且等于第三边的一半可得EF是△AND的中位线，然后根据三角形的中位线定理解答；
②当AM+BN=AD时，根据一组对边平行且相等的四边形是平行四边形可得四边形ANCM是平行四边形，再根据平行四边形的对边平行可得AN∥CM，同理可得BM∥DN，然后根据平行四边形的定义证明．

解答：（1）解：四边形MENF是平行四边形．
理由如下：在平行四边形ABCD中，AD=BC，
∵M，N分别为AD，BC的中点，
∴AM=

1

2

AD，CN=

1

2

BC，
∴AM=CN，
又∵AD∥BC，
∴四边形ANCM是平行四边形，
∴AN∥CM，
同理可得BM∥DN，
∴四边形MENF是平行四边形；

（2）解：①当AM=BN时，一定有EF

∥

.

1

2

AD．
理由如下：∵AM=BM，
∴DM=NC，
在△AEM和△NEB中
∵

∠MAE=∠ENB AM=BN ∠AME=∠NBE

，
∴△AEM≌△NEB（ASA），
∴DF=NF，
同理可得出：ME=BE，
∴EF是△AND的中位线，
∴EF

∥

.

1

2

AD；

②当AM+BN=AD时，四边形MENF为平行四边形．
理由如下：在平行四边形ABCD中，AD=BC，
∵AM+BN=AD，BN+CN=BC，
∴AM=CN，
又∵AD∥BC，
∴四边形ANCM是平行四边形，
∴AN∥CM，
同理可得BM∥DN，
∴四边形MENF是平行四边形．

点评：本题考查了平行四边形的判定与性质，三角形的中位线平行于第三边并且等于第三边的一半，熟记平行四边形性质和判定方法以及平行四边形的定义是解题的关键．