题目内容
某商场购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,根据销售经验,售价每提高一元,销售量相应减少十个,设每个篮球销售单价为x元,每个月销售利润为y元
(1)销售每个篮球所获利润为 元,这种篮球每月销售量为 个;
(2)求y与x的函数关系式;
(3)每个篮球销售单价为多少元时,每个月可获得最大利润?最大利润是多少元?
(1)销售每个篮球所获利润为
(2)求y与x的函数关系式;
(3)每个篮球销售单价为多少元时,每个月可获得最大利润?最大利润是多少元?
考点:二次函数的应用
专题:
分析:(1)依题意得销售每个篮球所获得的利润是(x-40)元,这种篮球每月的销售量是500-10(x-50),再整理即可,
(2)设月销售利润为y元,由题意得:y=(x-40)(1000-10x),再整理即可,
(3)根据(2)的结果,求出最大值即可.
(2)设月销售利润为y元,由题意得:y=(x-40)(1000-10x),再整理即可,
(3)根据(2)的结果,求出最大值即可.
解答:解:(1)依题意得销售每个篮球所获得的利润是(x-40)元,这种篮球每月的销售量是500-10(x-50)=(1000-10x)个;
故答案为:x-40,1000-10x,
(2)设月销售利润为y元,由题意得:y=(x-40)(1000-10x)=-10(x-70)2+9000,
(3)当x=70时,y有最大值9000;
答:每个篮球销售单价为70元时,每个月可获得最大利润,最大利润是9000元.
故答案为:x-40,1000-10x,
(2)设月销售利润为y元,由题意得:y=(x-40)(1000-10x)=-10(x-70)2+9000,
(3)当x=70时,y有最大值9000;
答:每个篮球销售单价为70元时,每个月可获得最大利润,最大利润是9000元.
点评:本题考查了二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题,关键是根据题意求出函数关系式.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
| 1 |
| 3 |
A、
| ||
B、-
| ||
| C、3 | ||
| D、-3 |
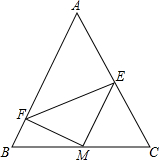 如图,在△ABC中,M是BC的中点,E,F分别在AC,AB上,且ME⊥MF.求证:EF<BF+CE.
如图,在△ABC中,M是BC的中点,E,F分别在AC,AB上,且ME⊥MF.求证:EF<BF+CE.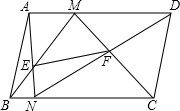 如图所示,在平行四边形ABCD中,M,N分别在AD,BC上,AN和BM交于点E,CM和DN交于点F,连结EF.
如图所示,在平行四边形ABCD中,M,N分别在AD,BC上,AN和BM交于点E,CM和DN交于点F,连结EF.