题目内容
已知方程k(x2-2x+1)-2x2+x=0有实数根,求k的取值范围.
考点:根的判别式,一元一次方程的解
专题:
分析:先把k(x2-2x+1)-2x2+x=0化成一般形式,再根据方程k(x2-2x+1)-2x2+x=0有实数根得出△=[-(2k-1)]2-4(k-2)k≥0且k≠2,最后整理即可.
解答:解:把k(x2-2x+1)-2x2+x=0整理得:
(k-2)x2-(2k-1)x+k=0,
∵方程k(x2-2x+1)-2x2+x=0有实数根,
∴△=[-(2k-1)]2-4(k-2)k≥0且k≠2,
解得k≥-
且k≠2.
(k-2)x2-(2k-1)x+k=0,
∵方程k(x2-2x+1)-2x2+x=0有实数根,
∴△=[-(2k-1)]2-4(k-2)k≥0且k≠2,
解得k≥-
| 1 |
| 4 |
点评:本题考查了根的判别式,用到的知识点是根的判别式、一元二次方程的定义,(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G.若∠CHE=125°,求∠FEG的度数.
如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G.若∠CHE=125°,求∠FEG的度数.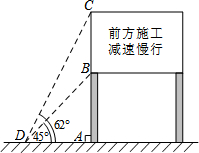 进入3月份,我市“两横三纵”快速路系统全线开工.为缓解市区内一些主要路段交通拥挤的现状,交警部门在一些主要路口设立了如图所示的交通路况显示牌.已知立杆AB的高度是3米,从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°.求路况显示牌BC的高度.(精确到0.1米)
进入3月份,我市“两横三纵”快速路系统全线开工.为缓解市区内一些主要路段交通拥挤的现状,交警部门在一些主要路口设立了如图所示的交通路况显示牌.已知立杆AB的高度是3米,从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°.求路况显示牌BC的高度.(精确到0.1米)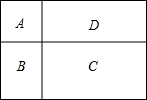 某农科站有一块长方形试验田,面积为1200m2.现要将其分为A、B、C、D四个区,其中A区为正方形.C区的长是30m,宽是20m.求A区的面积是多少平方米?
某农科站有一块长方形试验田,面积为1200m2.现要将其分为A、B、C、D四个区,其中A区为正方形.C区的长是30m,宽是20m.求A区的面积是多少平方米?