题目内容
用配方法证明:-9x2+8x-2<0.
考点:配方法的应用,非负数的性质:偶次方
专题:证明题
分析:先两前面两项提-9得到-9x2+8x-2=-9(x2-
x)-2,再利用配方法得到-9x2+8x-2=-9(x-
)2-
,然后根据非负数的性质进行证明.
| 8 |
| 9 |
| 4 |
| 9 |
| 2 |
| 9 |
解答:证明:-9x2+8x-2=-9(x2-
x)-2
=-9(x2-
x+
-
)-2
=-9(x-
)2-
,
∵9(x-
)2≥0,
∴-9(x-
)2-
≤0,
∴-9(x-
)2-
<0,
即-9x2+8x-2<0.
| 8 |
| 9 |
=-9(x2-
| 8 |
| 9 |
| 16 |
| 81 |
| 16 |
| 81 |
=-9(x-
| 4 |
| 9 |
| 2 |
| 9 |
∵9(x-
| 4 |
| 9 |
∴-9(x-
| 4 |
| 9 |
| 2 |
| 9 |
∴-9(x-
| 4 |
| 9 |
| 2 |
| 9 |
即-9x2+8x-2<0.
点评:本题考查了配方法的应用:用配方法解一元二次方程,配方法的理论依据是公式a2±2ab+b2=(a±b)2;利用配方法求二次三项式是一个完全平方式时所含字母系数的值.也考查了非负数的性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.
如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.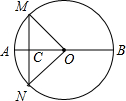 如图,AB是⊙O的直径,MN是弦,且AB⊥MN,若AB=4,且∠MON=90°,则MC=
如图,AB是⊙O的直径,MN是弦,且AB⊥MN,若AB=4,且∠MON=90°,则MC=