题目内容
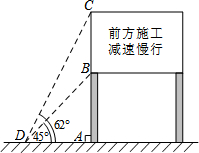 进入3月份,我市“两横三纵”快速路系统全线开工.为缓解市区内一些主要路段交通拥挤的现状,交警部门在一些主要路口设立了如图所示的交通路况显示牌.已知立杆AB的高度是3米,从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°.求路况显示牌BC的高度.(精确到0.1米)
进入3月份,我市“两横三纵”快速路系统全线开工.为缓解市区内一些主要路段交通拥挤的现状,交警部门在一些主要路口设立了如图所示的交通路况显示牌.已知立杆AB的高度是3米,从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°.求路况显示牌BC的高度.(精确到0.1米)(参考数据:sin62°=0.83,cos62°=0.47,tan62°=1.88)
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:在Rt△ADB中,根据∠BDA=45°,AD=AB=3,利用62°的正切函数解答即可.
解答:解:在Rt△ADB中,
∵∠BDA=45°,
∴AD=AB=3.
在Rt△ADC中,AC=ADtan62°=3×1.88=5.64.
BC=AC-AD=5.64-3=2.64≈2.6(米).
答:路况显示牌BC的高度是2.6米.
∵∠BDA=45°,
∴AD=AB=3.
在Rt△ADC中,AC=ADtan62°=3×1.88=5.64.
BC=AC-AD=5.64-3=2.64≈2.6(米).
答:路况显示牌BC的高度是2.6米.
点评:本题考查了解直角三角形--仰角俯角问题,找到未知量所在的直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.
如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.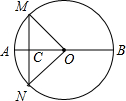 如图,AB是⊙O的直径,MN是弦,且AB⊥MN,若AB=4,且∠MON=90°,则MC=
如图,AB是⊙O的直径,MN是弦,且AB⊥MN,若AB=4,且∠MON=90°,则MC= 在菱形ABCD中,对角线AC、BD交于点O,AC、BD的长分别为5厘米、10厘米,则菱形ABCD的面积为
在菱形ABCD中,对角线AC、BD交于点O,AC、BD的长分别为5厘米、10厘米,则菱形ABCD的面积为