题目内容
11.如图1是长方形纸带,∠DEF=10°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE度数是多少( )
| A. | 110° | B. | 120° | C. | 150° | D. | 160° |
分析 由矩形的性质可知AD∥BC,由此可得出∠BFE=∠DEF=10°,再根据翻折的性质可知每翻折一次减少一个∠BFE的度数,由此即可算出∠CFE度数.
解答 解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=10°.
由翻折的性质可知:
∠EFC=180°-∠BFE=170°,∠BFC=∠EFC-∠BFE=160°,∠CFE=∠BFC-∠BFE=150°.
故选C.
点评 本题考查了翻折变换以及矩形的性质,解题的关键是找出∠CFE=180°-3∠BFE.本题属于基础题,难度不大,解决该题型题目时,根据翻折变换找出相等的边角关系是关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
6. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,∠EFB=60°,则△EFB′的面积是( )
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,∠EFB=60°,则△EFB′的面积是( )
 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,∠EFB=60°,则△EFB′的面积是( )
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,∠EFB=60°,则△EFB′的面积是( )| A. | 2 | B. | 4 | C. | 8$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
 如图,方格纸每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,点A(1,0),B(5,0),C(3,3),D(1,4).
如图,方格纸每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,点A(1,0),B(5,0),C(3,3),D(1,4).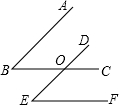 如图,已知BC、DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E,请你以其中两个判断作为条件,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.
如图,已知BC、DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E,请你以其中两个判断作为条件,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明. 已知函数y=ax+b与y=cx+d的图象如图所示,则关于x的不等式ax+b≥cx+d的解集是x≥2.
已知函数y=ax+b与y=cx+d的图象如图所示,则关于x的不等式ax+b≥cx+d的解集是x≥2.