题目内容
8．下列命题中，是假命题的是（ ）| A． | 对顶角相等 | B． | 同旁内角互补 | ||
| C． | 直角三角形的两个锐角互余 | D． | 两点确定一条直线 |
分析 利用对顶角的性质、平行线的性质、直角三角形的性质及确定直线的条件即可确定正确的选项．
解答 解：A、对顶角相等，正确，是真命题；
B、两直线平行，同旁内角互补，故错误，是假命题；
C、直角三角形的两个锐角相等，正确，为真命题；
D、两点确定一条直线，正确，是真命题，
故选B．
点评 本题考查了命题与定理的知识，解题的关键是能够了解对顶角的性质、平行线的性质、直角三角形的性质及确定直线的条件，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
已知：如图，在平面直角坐标系xOy中，直线AB分别与x、y轴交于点B、A，与反比例函数的$y=\frac{k}{x}$图象分别交于点C、D，CE⊥x轴于点E，$tan∠ABO=\frac{1}{2}$，OB=4，OE=2．
如图，在等边△ABC中，O为BC边上一点，E为AC边上一点，且∠ADE=6O°，BD=3，CE=2，则AB的长为9．
如图，△ABC中，D、E分别是AB、AC上的点，且BD=2AD，CE=2AE．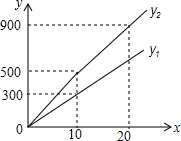
为发展旅游经济，我市某景区对门票采用灵活的售票方法吸引游客．门票定价为50元/人，非节假日打a折售票，节假日按团队人数分段定价售票，即m人以下（含m人）的团队按原价售票；超过m人的团队，其中m人仍按原价售票，超过m人部分的游客打b折售票．设某旅游团人数为x人，非节假日购票款为y1（元），节假日购票款为y2（元）．y1与y2之间的函数图象如图所示．
已知，如图，△ABC的顶点坐标分别为A（-2，3），B（-6，0），C（-1，0）．
20．
如图，已知线段AB两个端点的坐标分别为A（6，6），B（8，4），以原点O为位似中心，在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD，则端点D的坐标为（ ）
如图，已知线段AB两个端点的坐标分别为A（6，6），B（8，4），以原点O为位似中心，在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD，则端点D的坐标为（ ）| A． | （4，2） | B． | （2，4） | C． | （3，3） | D． | （4，2）或（-4，2） |
17．从3，4，5三个数中随机抽取两个数，则取出的两个数都是奇数的概率为（ ）
| A． | 0 | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | 1 |
18．若关于x，y的方程组$\left\{\begin{array}{l}{3x+ky=-3k+2}\\{4x-y=3}\end{array}\right.$的解满足2x+y=9，则k=（ ）
| A． | -1 | B． | 2 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |