题目内容
19．下列说法正确的是（ ）| A． | 同圆或等圆中，等现所对的圆周角相等 | |
| B． | 圆的切线垂直于半径 | |
| C． | 三角形的内心是三角形角平分线的交点 | |
| D． | 平分弦的直径垂直于弦 |
分析 由于同圆或等圆中，同一条弦对两种不同的圆周角，则可对A进行判断；根据切线的性质对B进行判断；根据三角形内心的定义对C进行判断；根据垂径定理的推论对D进行判断．
解答 解：A、同圆或等圆中，等弦所对的圆周角相等或互补，所以A选项错误；
B、圆的切线垂直于过切点的半径，所以B选项错误；
C、三角形的内心是三角形角平分线的交点，所以C选项正确；
D、平分弦（非直径）的直径垂直于弦，所以D选项错误．
故选C．
点评 本题考查了三角形的内切圆与内心：三角形的内心就是三角形三个内角角平分线的交点．三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．也考查了圆周角定理和垂径定理．
练习册系列答案
相关题目
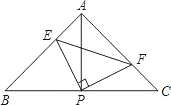已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE，PF分别交AB，AC于点E，F，给出以下结论：
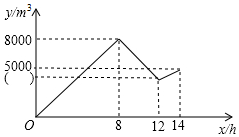某企业一地下仓库发生渗水事故，凌晨0点开始渗漏，工作人员发现后于8点开始使用4台相同的抽水机排水，4小时后由于电路出现故障，为保证安全，有3台抽水机停止工作，2小时后电路故障仍然未完全排除，仅有两台抽水机恢复了工作，假设每小时的渗水量相同，仓库中的剩余水量不超过1000m3时才能对渗漏处进行封堵，仓库中存水量y（单位：m3）关于漏水时间x（单位：h）的函数图象如图所示．