题目内容
9.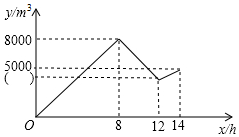 某企业一地下仓库发生渗水事故,凌晨0点开始渗漏,工作人员发现后于8点开始使用4台相同的抽水机排水,4小时后由于电路出现故障,为保证安全,有3台抽水机停止工作,2小时后电路故障仍然未完全排除,仅有两台抽水机恢复了工作,假设每小时的渗水量相同,仓库中的剩余水量不超过1000m3时才能对渗漏处进行封堵,仓库中存水量y(单位:m3)关于漏水时间x(单位:h)的函数图象如图所示.
某企业一地下仓库发生渗水事故,凌晨0点开始渗漏,工作人员发现后于8点开始使用4台相同的抽水机排水,4小时后由于电路出现故障,为保证安全,有3台抽水机停止工作,2小时后电路故障仍然未完全排除,仅有两台抽水机恢复了工作,假设每小时的渗水量相同,仓库中的剩余水量不超过1000m3时才能对渗漏处进行封堵,仓库中存水量y(单位:m3)关于漏水时间x(单位:h)的函数图象如图所示.(1)求每小时的渗水量和每台抽水机每小时的排水量;
(2)图中括号中应填4000;
(3)求出仅剩一台抽水机单独工作时y关于x的函数解析式;
(4)若计划20点开始封堵,是否能够实现?若能实现,请说明理由,若不能实现,请直接写出最后一台抽水机最迟要在几点恢复工作才能保证在20点开始封堵.
分析 (1)根据前八个小时的总渗水量除以8,即可求出每小时的渗水量,再根据减少的渗水量及抽水机工作的台数及时间,即可求出每台抽水机每小时的排水量;
(2)由8000+4小时的渗水量-4台抽水机4小时的抽水量,即可求出当x=12时y值;
(3)观察函数图象,找出点的坐标,利用待定系数法求出仅剩一台抽水机单独工作时y关于x的函数解析式;
(4)找出当x>14时,y关于x的函数解析式,利用一次函数图象上点的坐标特征求出当x=20时y的值,比较后即可得出不能实现,再用相差的排水量除以一台抽水机每小时的排水量结合时间,即可求出结论.
解答 解:(1)8000÷8=1000(m3),
[1000×(14-8)+8000-5000]÷(4×4+1×2)=500(m3).
答:每小时的渗水量为1000m3,每台抽水机每小时的排水量为500m3.
(2)8000-500×4×4+1000×4=4000(m3).
故答案为:4000.
(3)设仅剩一台抽水机单独工作时y关于x的函数解析式为y=kx+b,
将(12,4000)、(14,5000)代入y=kx+b中,
$\left\{\begin{array}{l}{12k+b=4000}\\{14k+b=5000}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=500}\\{b=-2000}\end{array}\right.$,
∴仅剩一台抽水机单独工作时y关于x的函数解析式为y=500x-2000.
(4)当x>14时,y=5000-(3×500-1000)×(x-14)=-500x+12000,
当x=20时,y=2000,
∵2000>1000,
∴若计划20点开始封堵,不能实现.
20-(2000-1000)÷500=18(时).
答:最后一台抽水机最迟要在18点恢复工作才能保证在20点开始封堵.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,解题的关键是:(1)根据数量关系,列式计算;(2)根据数量关系,列式计算;(3)根据点的坐标,利用待定系数法求出函数解析式;(4)根据一次函数图象上点的坐标特征,求出当x=20时y值.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | 同圆或等圆中,等现所对的圆周角相等 | |
| B. | 圆的切线垂直于半径 | |
| C. | 三角形的内心是三角形角平分线的交点 | |
| D. | 平分弦的直径垂直于弦 |
为了了解某市初中生的视力情况,随机抽取了3000名学生进行检测,收集数据后,绘制了以下三幅统计图表,请根据图表中提供的信息解答下列问题:
| 调查人数 | 视力不良 | 视力不良率(精确到0.01) | |
| 男生 | 1400 | 750 | 54% |
| 女生 | 1600 | m | n |
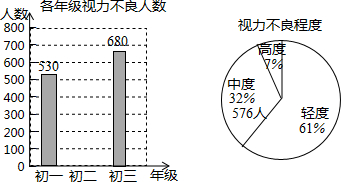
根据统计图表回答下列问题:
(1 )统计表中m=1050,n=66%;
(2)补全条形统计图,并通过计算估计该市80000名初中生的视力不良情况的人数;
(3)通过统计图表中的信息,写出一条关于视力不良的正确结论.
| x(元) | 200 | 240 | 270 | 300 |
| y(间) | 90 | 70 | 55 | 40 |
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入-当日支出)
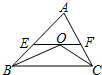 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )| A. | 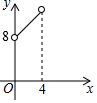 | B. | 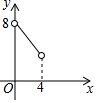 | C. | 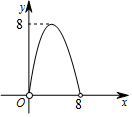 | D. | 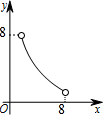 |
 如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )| A. | 100° | B. | 80° | C. | 60° | D. | 40° |