题目内容
10. 如图,在△ABC中,∠C=90°,∠BAC=30°,AB=8,AD平分∠BAC,点PQ分别是AB、AD边上的动点,则PQ+BQ的最小值是( )
如图,在△ABC中,∠C=90°,∠BAC=30°,AB=8,AD平分∠BAC,点PQ分别是AB、AD边上的动点,则PQ+BQ的最小值是( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 如图,作点P关于直线AD的对称点P′,连接QP′,由△AQP≌△AQP′,得PQ=QP′,欲求PQ+BQ的最小值,只要求出BQ+QP′的最小值,即当BP′⊥AC时,BQ+QP′的值最小,此时Q与D重合,P′与C重合,最小值为BC的长.
解答 解:如图,作点P关于直线AD的对称点P′,连接QP′,
在△AQP和△AQP′中,
$\left\{\begin{array}{l}{AP=AP′}\\{∠QAP=∠QAP′}\\{AQ=AQ}\end{array}\right.$,
∴△AQP≌△AQP′,
∴PQ=QP′
∴欲求PQ+BQ的最小值,只要求出BQ+QP′的最小值,
∴当BP′⊥AC时,BQ+QP′的值最小,此时Q与D重合,P′与C重合,最小值为BC的长.
在Rt△ABC中,∵∠C=90°,AB=8,∠BAC=30°,
∴BC=$\frac{1}{2}$AB=4,
∴PQ+BQ的最小值是4,
故选A.
点评 本题考查了勾股定理、轴对称中的最短路线问题、垂线段最短等知识,找出点P、Q的位置是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
19.立方是它本身的数是( )
| A. | 1 | B. | 0 | C. | -1 | D. | 1,-1,0 |
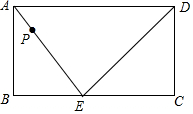 如图,在矩形ABCD中,点E在BC边上,动点P以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从A出发经x(x>0)秒后,△ABP的面积是y.
如图,在矩形ABCD中,点E在BC边上,动点P以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从A出发经x(x>0)秒后,△ABP的面积是y.
 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是在角的内部,到角两边距离相等的点在角的平分线上.
小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是在角的内部,到角两边距离相等的点在角的平分线上.