题目内容
12．
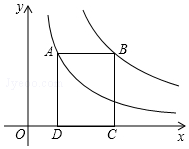如图，点A在双曲线y=$\frac{4}{x}$上，点B在双曲线y=$\frac{k}{x}$（k≠0）上，AB∥x轴，分别过点A、B向x轴作垂线，垂足分别为D、C，若矩形ABCD的面积是9，则k的值为（ ）| A． | 4 | B． | 5 | C． | 9 | D． | 13 |
分析 首先得出矩形EODA的面积为：4，利用矩形ABCD的面积是9，则矩形EOCB的面积为：4+9=13，再利用xy=k求出即可．
解答 
解：过点A作AE⊥y轴于点E，
∵点A在双曲线y=$\frac{4}{x}$上，
∴矩形EODA的面积为：4，
∵矩形ABCD的面积是9，
∴矩形EOCB的面积为：4+9=13，
则k的值为：xy=k=13．
故选D．
点评 此题主要考查了反比例函数关系k的几何意义，得出矩形EOCB的面积是解题关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
2．甲、乙两人同时从A地出发，骑自行车到B地，已知A、B两地的距离为50km，甲每小时比乙每小时多走2km，并且比乙先到20分钟，设乙每小时走xkm，则可列方程为（ ）
| A． | $\frac{50}{x}$-$\frac{50}{x-2}$=$\frac{1}{3}$ | B． | $\frac{50}{x}$-$\frac{50}{x+2}$=$\frac{1}{3}$ | C． | $\frac{50}{x+2}$-$\frac{50}{x}$=$\frac{1}{3}$ | D． | $\frac{50}{x-2}$-$\frac{50}{x}$=$\frac{1}{3}$ |
用五块大小相同的小正方体搭成如图所示的几何体，这个几何体的俯视图是（ ）
20．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
17．
如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下面四个结论：①OA=OD；②AD⊥EF；③当∠BAC=90°时，四边形AEDF是正方形；④AE2+DF2=AF2+DE2．其中正确的是（ ）
如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下面四个结论：①OA=OD；②AD⊥EF；③当∠BAC=90°时，四边形AEDF是正方形；④AE2+DF2=AF2+DE2．其中正确的是（ ）| A． | ②③ | B． | ②④ | C． | ②③④ | D． | ①③④ |
4．下列运算正确的是（ ）
| A． | （a+b）2=a2+b2 | B． | a8÷a4=a2 | C． | 2a+3b=5ab | D． | a2•a3=a5 |
1．若二次根式$\sqrt{3x-2}$有意义，则x的取值范围是（ ）
| A． | x≥$\frac{2}{3}$ | B． | x≤$\frac{2}{3}$ | C． | x≥$\frac{3}{2}$ | D． | x≤$\frac{3}{2}$ |
2．定义新运算“⊕”如下：当a＞b时，a⊕b=ab+b；当a＜b时，a⊕b=ab-b，若3⊕（x+2）＞0，则x的取值范围是（ ）
| A． | -1＜x＜1或x＜-2 | B． | x＜-2或1＜x＜2 | C． | -2＜x＜1或x＞1 | D． | x＜-2或x＞2 |