题目内容
3.经过某丁字路口的汽车,它可能左转或右转,如果这两种可能性大小相同,同向而行的三辆汽车都经过这个丁字路口时,求下列事件的概率:(1)第一辆车向左转的概率是$\frac{1}{2}$;
(2)请画出三辆车转弯的树形图,并根据树形图求三辆车中,至少有两辆车朝两个不同方向转弯的概率是多少.
分析 (1)直接利用概率公式求解;
(2)画树状图展示所有9种等可能的结果数,再找出至少有两辆车朝两个不同方向转弯的结果数,然后根据概率公式计算.
解答 解:(1)第一辆车向左转的概率为$\frac{1}{2}$;
故答案为$\frac{1}{2}$;
(2)画树状图为:
共有8种等可能的结果数,至少有两辆车朝两个不同方向转弯的结果数为6,
所以至少有两辆车朝两个不同方向转弯的概率=$\frac{6}{8}$=$\frac{3}{4}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
11.某商店购进了A,B两种家用电器,相关信息如下表:
已知用6000元购进的A种电器件数与用5000元购进的B种电器件数相同.
(1)求表中m的值.
(2)由于A,B两种家用电器热销,该商店计划用不超过23000元的资金再购进A,B两种电器总件数共20件,且获利不少于13300元.请问:有几种进货方案?哪一种方案才能获得最大利润?最大利润是多少?
| 家用电器 | 进价(元/件) | 售价(元/件) |
| A | m+200 | 1800 |
| B | m | 1700 |
(1)求表中m的值.
(2)由于A,B两种家用电器热销,该商店计划用不超过23000元的资金再购进A,B两种电器总件数共20件,且获利不少于13300元.请问:有几种进货方案?哪一种方案才能获得最大利润?最大利润是多少?
12. 如图所示,AB是⊙O的直径,C,D为圆上两点,若∠D=30°,则∠AOC等于( )
如图所示,AB是⊙O的直径,C,D为圆上两点,若∠D=30°,则∠AOC等于( )
 如图所示,AB是⊙O的直径,C,D为圆上两点,若∠D=30°,则∠AOC等于( )
如图所示,AB是⊙O的直径,C,D为圆上两点,若∠D=30°,则∠AOC等于( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |

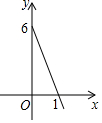 某登山队大本营所在地的气温为6℃,海拔每升高1km气温下降6℃,登山队由大本营向上登高xkm时他们所在位置的气温是y℃,表示y与x关系的图象如图所示.
某登山队大本营所在地的气温为6℃,海拔每升高1km气温下降6℃,登山队由大本营向上登高xkm时他们所在位置的气温是y℃,表示y与x关系的图象如图所示.