题目内容
11.某商店购进了A,B两种家用电器,相关信息如下表:| 家用电器 | 进价(元/件) | 售价(元/件) |
| A | m+200 | 1800 |
| B | m | 1700 |
(1)求表中m的值.
(2)由于A,B两种家用电器热销,该商店计划用不超过23000元的资金再购进A,B两种电器总件数共20件,且获利不少于13300元.请问:有几种进货方案?哪一种方案才能获得最大利润?最大利润是多少?
分析 (1)根据“用6000元购进的A种电器件数与用5000元购进的B种电器件数相同”列分式方程求解可得;
(2)设计划购进A种电器件数为x,根据购进总钱数不超过23000元及获利不少于13300元求得x的范围,依据题意列出总利润y关于x的函数关系式,利用一次函数的性质求解可得.
解答 解:(1)由题意可得:
$\frac{6000}{m+2}$=$\frac{5000}{m}$,
解得:m=1000,
经检验得:m=1000是原方程的根,
答:m的值为1000;
(2)设计划购进A种电器件数为x,则
$\left\{\begin{array}{l}{1200x+1000(20-x)≤23000}\\{600x+700(20-x)≥13300}\end{array}\right.$,
解得:x≤7,
则x可取的整数有0、1、2、3、4、5、6、7这8种,
故购进方案有8种,
设所获利润为y,
则y=600x+700(20-x)=-100x+14000,
∵y随x的增大而减小,
∴当x=0时,y取得最大值,最大值为14000元,
即进货方案为A种电器0台,B种电器20台时,利润最大,最大利润为14000元.
点评 本题主要考查分式方程和一元一次不等式及一次函数的应用,理解题意找到题目蕴含的相等关系或不等关系列出方程、不等式组及函数解析式式解题的关键.

练习册系列答案
相关题目
20.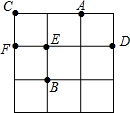 如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任意取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是( )
如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任意取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是( )
 如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任意取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是( )
如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任意取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是( )| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
1.某玩具厂有A种塑料70吨,B种塑料52吨,现利用两种塑料生产M,N两型滑梯80套,其中一套M型滑梯用A种塑料0.6吨,B种塑料0.9吨,可获利4500元;做一套N型滑梯需要A种塑料1.1吨,B中塑料0.4吨,可获利5000元,若设生产N型滑梯x套,用这些塑料生产这两种滑梯所获总利为y元.
(1)填写表内空格:
(2)N型滑梯的数量应控制在什么范围内?
(3)求y与x的函数关系式.
(4)生产N型滑梯多少套时所获利润最大?最大利润是多少?
(1)填写表内空格:
| 套 | A种塑料(吨) | B种塑料(吨) | |
| M型滑梯 | 80-x | 0.6(80-x) | 0.9(80-x) |
| N型滑梯 | x | 1.1x | 0.4x |
| 合计 | 80 | 70 | 52 |
(3)求y与x的函数关系式.
(4)生产N型滑梯多少套时所获利润最大?最大利润是多少?
 如图,AB是⊙O直径,C、D是弧AB的三等分点,P为直径AB上一点,若AB=12,则图中阴影部分的面积为6π.
如图,AB是⊙O直径,C、D是弧AB的三等分点,P为直径AB上一点,若AB=12,则图中阴影部分的面积为6π. 如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护的问题的电话最多,共70个,请回答下列问题.
如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护的问题的电话最多,共70个,请回答下列问题.