题目内容
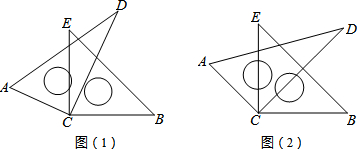
 如图,AD平分∠EAC.
如图,AD平分∠EAC.(1)若∠B=50°,AD∥BC,则∠DAC=
(2)若∠C=55°,∠EAC=110°,AD与BC平行吗?为什么?
根据解答过程填空(填理由或数学式).
解:∵AD平分∠EAC(已知)
∴∠DAC=
| 1 |
| 2 |
∵∠C=55°(已知)
∴∠C=∠
∴AD∥BC
考点:平行线的判定与性质
专题:推理填空题
分析:(1)根据角平分线定义求出∠EAD=∠DAC,根据平行线的性质得出∠EAD=∠B,即可得出答案;
(2)根据角平分线定义求出∠DAC,求出∠C=∠DAC,根据平行线的判定得出即可.
(2)根据角平分线定义求出∠DAC,求出∠C=∠DAC,根据平行线的判定得出即可.
解答:解:(1)∵AD平分∠EAC,
∴∠EAD=∠DAC,
∵AD∥BC,∠B=50°,
∴∠EAD=∠B=50°,
∴∠DAC=50°,
故答案为:50;
(2)∵AD平分∠EAC(已知),
∴∠DAC=
∠EAC=55°(角平分线的定义),
∵∠C=55°(已知),
∴∠C=∠DAC((等量代换),
∴AD∥BC(内错角相等,两直线平行),
故答案为:55,DAC,(内错角相等,两直线平行).
∴∠EAD=∠DAC,
∵AD∥BC,∠B=50°,
∴∠EAD=∠B=50°,
∴∠DAC=50°,
故答案为:50;
(2)∵AD平分∠EAC(已知),
∴∠DAC=
| 1 |
| 2 |
∵∠C=55°(已知),
∴∠C=∠DAC((等量代换),
∴AD∥BC(内错角相等,两直线平行),
故答案为:55,DAC,(内错角相等,两直线平行).
点评:本题考查了平行线的性质和判定的应用,注意:两直线平行,同位角相等,反之亦然.

练习册系列答案
相关题目
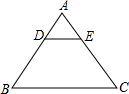 如图,△ABC是等腰三角形,顶点为A、D、E分别在腰AB、AC上,连接DE,若△ADE是等腰三角形,且顶点为A,则下列结论中错误的是( )
如图,△ABC是等腰三角形,顶点为A、D、E分别在腰AB、AC上,连接DE,若△ADE是等腰三角形,且顶点为A,则下列结论中错误的是( )| A、AD=AE |
| B、BD=CE |
| C、DE∥BC |
| D、△ADE≌△ABC |
抛物线y=
(x-2)2+3的对称轴是直线( )
| 1 |
| 2 |
| A、x=-2 | B、x=2 |
| C、x=3 | D、x=-3 |
| 1 |
| 2 |
| 3 |
| 2015 |
| 5 |
| A、18个 | B、19个 |
| C、20个 | D、21个 |
 如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.
如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.