题目内容

6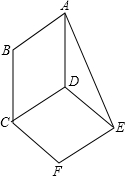．如图，?ABCD与?DCFE的周长相等，且∠BAD=60°，∠F=100°，则∠DAE的度数为（　　）
A．20°B．25°C．30°D．35°

分析 由?ABCD与?DCFE的周长相等，可得到AD=DE即△ADE是等腰三角形，再由且∠BAD=60°，∠F=100°，即可求出∠DAE的度数．

解答 解：∵?ABCD与?DCFE的周长相等，且CD=CD，
∴AD=DE，
∵∠DAE=∠DEA，
∵∠BAD=60°，∠F=100°，
∴∠ADC=120°，∠CDE═∠F=100°，
∴∠ADE=360°-120°-100°=140°，
∴∠DAE=（180°-140°）÷2=20°，
故选：A．

点评 本题考查了平行四边形的性质：平行四边形的对边相等、平行四边形的对角相等以及邻角互补和等腰三角形的判定和性质、三角形的内角和定理．

练习册系列答案
相关题目
16．如图，已知△ABC，△HMB，△BDG均为等边三角形，其中点C，D，H，M在x轴上，点B在y轴上，过点G作GF⊥直线HB于点F，过点A作AE⊥直线MB于点E．
（1）当点A与点G重合于y轴时，如图1，则GF=AE（填“＜”“＞”或“=”），∠EGF=120°．
（2）如图2．
①判断GF与AE的大小关系，并证明；
②已知点C（c，0），D（d，0），B（0，b）用含b、c、d的式子表示S△AEB+S△BFG；
③若直线AE与直线FG相交所夹的较大角为α，请直接判断α是否会随着三个等边三角形（△ABC，△HMB，△BDG）的大小改变而改变．
17．下列说法正确的是（　　）
A．等角的补角相等B．相等的角是对顶角
C．和为180°的两角互余D．内错角互补，两直线平行
14．汶川地震发生后某市组织了20辆汽车装运食品、药品、生活用品三种救灾物资共100吨到灾民安置点．按计划20辆汽车都要装运，每辆汽车只能装运同一种救灾物资且必须装满．根据下表提供的信息，解答下列问题：
物资种类食品药品生活用品
每辆汽车装载量/吨654
每吨所需运费/元/吨120160100
（1）设装运食品的车辆数为x辆，装运药品的车辆数为y辆．求y与x的函数关系式；
（2）如果装运食品的车辆数不少于5辆，装运药品的车辆数不少于4辆，那么，车辆的安排有几种方案？并写出每种安排方案；
（3）在（2）的条件下，若要求总运费最少，应采用哪种安排方案？并求出最少总运费．
1．（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E，证明：DE=BD+CE．
（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请直接写出线段DE、BD、CE之间的数量关系（不要求说明理由）；
（3）将（1）中的直线m绕点A旋转，使其与BC边相交，则结论DE=BD+CE是否还成立？如成立，请你给出证明；若不成立，请写出所有可能的结论，并在图3中画出相应的图形．
11．“a与b的平方和不小于它们积的2倍”正确的表示方法是（　　）
A．a2+b2＞2abB．a2+b2≥2abC．（a+b）2＞2abD．（a+b）2≥2ab
18．某洗衣机的洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程．其中进水、清洗、排水时洗衣机中的水量y（升）与时间x（分钟）之间的关系如图所示．根据图象解答下列问题：
（1）在这个变化过程中，自变量、因变量各是什么？
（2）洗衣机的进水时间是多少分钟？清洗时洗衣机中的水量是多少升？
（3）若排水速度与进水速度相同，那么
①洗衣机清洗衣服所用的时间是多少分钟？
②求洗衣机排水时水量y（升）与时间x（分钟）之间的关系式．
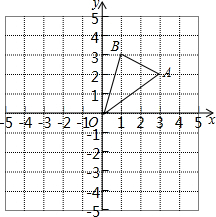15．如图，边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2），B（1，3）．
（1）写出△AOB的面积为3.5；
（2）点P在x轴上，当PA+PB的值最小时，在图中画出点P，并求出点P的坐标．
16．2003年6月1日，举世瞩目的三峡工程正式下闸蓄水，26台发电机组发电量达84700000000千瓦时，用科学记数法表示应为8.47×1010千瓦时．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网