题目内容
13.已知方程3x2-2x-4=0,求一个一元二次方程,使它的两根分别为已知方程各根的平方.分析 设方程3x2-2x-4=0的两根分别为a、b,根据根与系数的关系得到a+b=$\frac{2}{3}$,ab=-$\frac{4}{3}$,再计算a2+b2和a2•b2的值,然后根据根与系数的关系写出新方程.
解答 解:设方程3x2-2x-4=0,的两根分别为a、b,则a+b=$\frac{2}{3}$,ab=-$\frac{4}{3}$,
∵a2+b2=(a+b)2-2ab=$\frac{4}{9}$-2×(-$\frac{4}{3}$)=$\frac{28}{9}$,
a2•b2=(a•b)2=$\frac{16}{9}$,
∴所求的新方程为x2-$\frac{28}{9}$x+$\frac{16}{9}$=0,
即:所求的新方程为9x2-28x+16=0.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
4.可用来表示13的立方根的是( )
| A. | $\sqrt{13}$ | B. | $\root{3}{13}$ | C. | ±$\sqrt{13}$ | D. | ±$\root{3}{13}$ |
 如图,点D、E分别在△ABC的边AB、AC上,∠ADE=∠ACB,求证:∠AED=∠ABC.
如图,点D、E分别在△ABC的边AB、AC上,∠ADE=∠ACB,求证:∠AED=∠ABC.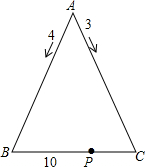 如图,有两只蚂蚁同时从一个等腰三角形的顶点A出发,先分别沿两腰爬行,速度分别为4厘米/秒,3厘米/秒,7秒后在离点B处10厘米的点P相遇,求PC的长.
如图,有两只蚂蚁同时从一个等腰三角形的顶点A出发,先分别沿两腰爬行,速度分别为4厘米/秒,3厘米/秒,7秒后在离点B处10厘米的点P相遇,求PC的长. 如图,利用网格线画出图中∠ACB的平分线和线段BC的垂直平分线,设两条线的交点为P,试说明与点P有关的正确结论.
如图,利用网格线画出图中∠ACB的平分线和线段BC的垂直平分线,设两条线的交点为P,试说明与点P有关的正确结论. 已知,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.
已知,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.