题目内容
5.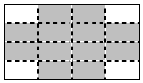 把正整数1,2,3,4,…,2014排列成如图所示的一个表
把正整数1,2,3,4,…,2014排列成如图所示的一个表| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 … |
(2)没有被阴影覆盖的这四个数之和能等于96吗?若能,请求出x的值;若不能,请说明理由.
(3)那这四个数之和又能否等于3282呢?如果能,请求出x的值;如果不能,请说明理由.
分析 (1)观察数列的排列方式即可得出:每行有8个数,同行相邻两列数差为1,同列相邻两行的差为8.根据最小的数为x结合正方形的性质即可得出其它三个数;
(2)根据(1)将此四个数相加,令其等于96即可得出关于x的一元一次方程,解之即可求出x的值,由x不是正整数即可得出这四个数之和不能等于96;
(3)根据(1)将此四个数相加,令其等于3282即可得出关于x的一元一次方程,解之即可求出x的值,由x为正整数即可得出结论.
解答 解:(1)观察数列可知:每行有8个数,同行相邻两列数差为1,同列相邻两行的差为8.
∵最小的数记为x,
∴另外三个数分别为:x+3,x+24,x+27.
故答案为:x+3;x+24;x+27.
(2)没有被阴影覆盖的这四个数之和不能等于96,理由如下:
四个数之和为x+x+3+x+24+x+27=4x+54,
∴4x+54=96,
解得:x=10.5,
∵x为正整数,
∴没有被阴影覆盖的这四个数之和不能等于96.
(3)根据题意得:4x+54=3282,
解得:x=807.
答:这四个数之和能等于3282,此时x的值为807.
点评 本题考查了一元一次方程的应用以及列代数式,解题的关键是:(1)根据数列的排列用含x的代数式表示其它三个数;(2)根据四个数之和为96列出关于x的一元一次方程;(3)根据四个数之和为3282列出关于x的一元一次方程.

练习册系列答案
相关题目
20.若m、n满足|2m+3|+(n-2)4=0,则mn的值等于( )
| A. | $\frac{9}{4}$ | B. | $\frac{3}{2}$ | C. | -$\frac{9}{4}$ | D. | 0 |
10.计算(2a)3•2a2的结果是( )
| A. | 16a5 | B. | 4a6 | C. | 8a5 | D. | 8a6 |
15.下列四个图形中,若∠1=∠2,能判断AB∥CD的是( )
| A. |  | B. |  | C. |  | D. |  |
 将下列各数表示在数轴上,并用“<”连接.
将下列各数表示在数轴上,并用“<”连接.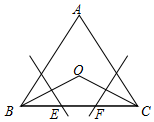 如图所示,在等边三角形ABC中,∠B、∠C的平分线交于点O,OB和OC的垂直平分线交BC于E、F,试用你所学的知识说明BE=EF=FC的道理.
如图所示,在等边三角形ABC中,∠B、∠C的平分线交于点O,OB和OC的垂直平分线交BC于E、F,试用你所学的知识说明BE=EF=FC的道理.