题目内容
20.若m、n满足|2m+3|+(n-2)4=0,则mn的值等于( )| A. | $\frac{9}{4}$ | B. | $\frac{3}{2}$ | C. | -$\frac{9}{4}$ | D. | 0 |
分析 根据非负数的性质列方程求出m、n的值,然后代入代数式进行计算即可得解.
解答 解:由题意得,2m+3=0,n-2=0,
解得m=-$\frac{3}{2}$,n=2,
所以,mn=(-$\frac{3}{2}$)2=$\frac{9}{4}$.
故选A.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
15.若正方形的对角线长为2cm,则这个正方形的面积为( )
| A. | 4 cm2 | B. | 2 cm2 | C. | $\sqrt{2}$cm2 | D. | 2$\sqrt{2}$cm2 |
5.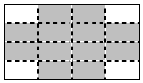 把正整数1,2,3,4,…,2014排列成如图所示的一个表
把正整数1,2,3,4,…,2014排列成如图所示的一个表
(1)用一正方形在表中随意框住16个数,把其中没有被阴影覆盖的最小的数记为x,另外没有被覆盖的数用含x的式子表示出来,从小到大依次是x+3、x+24、x+27.
(2)没有被阴影覆盖的这四个数之和能等于96吗?若能,请求出x的值;若不能,请说明理由.
(3)那这四个数之和又能否等于3282呢?如果能,请求出x的值;如果不能,请说明理由.
 把正整数1,2,3,4,…,2014排列成如图所示的一个表
把正整数1,2,3,4,…,2014排列成如图所示的一个表| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 … |
(2)没有被阴影覆盖的这四个数之和能等于96吗?若能,请求出x的值;若不能,请说明理由.
(3)那这四个数之和又能否等于3282呢?如果能,请求出x的值;如果不能,请说明理由.
12.下列从左到右的变形,属于因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | x2+2x=x(x+2) | C. | m2+m-4=m(m+1)-4 | D. | 2x2+2x=2x2(1+$\frac{1}{x}$) |
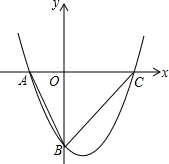 如图,抛物线y=x2-x-6交x轴于A、C两点,交y轴于点B;将抛物线y=x2-x-6向上平移$\frac{23}{4}$个单位长度、再向左平移m(m>0)个单位长度,得到新抛物线;若新抛物线的顶点P在△ABC内,则m的取值范围是0<m$<\frac{7}{3}$.
如图,抛物线y=x2-x-6交x轴于A、C两点,交y轴于点B;将抛物线y=x2-x-6向上平移$\frac{23}{4}$个单位长度、再向左平移m(m>0)个单位长度,得到新抛物线;若新抛物线的顶点P在△ABC内,则m的取值范围是0<m$<\frac{7}{3}$.