题目内容
3. 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.则C13的顶点坐标为( )
| A. | ($\frac{69}{2}$,$\frac{9}{4}$) | B. | ($\frac{69}{2}$,-$\frac{9}{4}$) | C. | ($\frac{75}{2}$,$\frac{9}{4}$) | D. | ($\frac{75}{2}$,-$\frac{9}{4}$) |
分析 求得C1的顶点坐标为($\frac{3}{2}$,$\frac{9}{4}$),根据顶点坐标的变换规律求得C2、C3、C4的顶点坐标,得出顶点变化规律即可得.
解答 解:∵y=-x(x-3)=-x2+3x=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$,
∴C1的顶点坐标为($\frac{3}{2}$,$\frac{9}{4}$),
由题意可得C2的顶点坐标为($\frac{3}{2}$×3,-$\frac{9}{4}$),
C3的顶点坐标为($\frac{3}{2}$×5,$\frac{9}{4}$),
C4的顶点坐标为($\frac{3}{2}$×7,-$\frac{9}{4}$),…
∴C13的顶点坐标为($\frac{3}{2}$×25,$\frac{9}{4}$),即($\frac{75}{2}$,$\frac{9}{4}$),
故选:C.
点评 本题主要考查抛物线与x轴的交点及二次函数图象与几何变换,根据图形的变换得出顶点的变化规律是解题的关键.

练习册系列答案
相关题目
13.下列分数中,能化成有限小数是( )
| A. | $\frac{7}{40}$ | B. | $\frac{1}{24}$ | C. | $\frac{4}{15}$ | D. | $\frac{5}{12}$ |
11.下列数中,不可能是某月相邻的三个日期之和的是( )
| A. | 24 | B. | 43 | C. | 57 | D. | 69 |
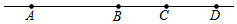 如图,一条直线上有四点A、B、C、D,以下说法:①图中共有6条线段;②若B为AD的中点,则$\frac{BC}{CA-CD}$=$\frac{1}{2}$;③若想在直线上找一点,使这个点到A、B、C、D四个点的距离之和最小,则这个点一定在线段BC上,其中正确的有①③.
如图,一条直线上有四点A、B、C、D,以下说法:①图中共有6条线段;②若B为AD的中点,则$\frac{BC}{CA-CD}$=$\frac{1}{2}$;③若想在直线上找一点,使这个点到A、B、C、D四个点的距离之和最小,则这个点一定在线段BC上,其中正确的有①③.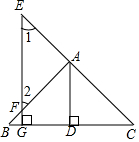 如图,点E、A、C在一条直线上,给出下列三个事项:①AD⊥BC,FG⊥BC,垂足分别为D、G;②∠1=∠2;③AD平分∠BAC.
如图,点E、A、C在一条直线上,给出下列三个事项:①AD⊥BC,FG⊥BC,垂足分别为D、G;②∠1=∠2;③AD平分∠BAC. 如图,在正方形ABCD内,∠AFB=∠CED=90°,AF=CE,连结EF,若EF=3$\sqrt{2}$,两块阴影部分的面积和为4,则正方形ABCD的面积为( )
如图,在正方形ABCD内,∠AFB=∠CED=90°,AF=CE,连结EF,若EF=3$\sqrt{2}$,两块阴影部分的面积和为4,则正方形ABCD的面积为( )