题目内容
12. 如图,在正方形ABCD,E、F分别为DC、BC中点,求证:△ADE≌△ABF.
如图,在正方形ABCD,E、F分别为DC、BC中点,求证:△ADE≌△ABF.
分析 欲证明△ADE≌△ABF,只要证明AD=AB,∠D=∠B,DE=BF即可.
解答 证明: ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=AD=CD=BC,∠B=∠D=90°,
∵DE=EC,FB=FC,
∴DE=BF,
在△AED和△AFB中,
$\left\{\begin{array}{l}{AD=AB}\\{∠D=∠B}\\{DE=BF}\end{array}\right.$,
∴△ADE≌△ABF.
点评 本题考查正方形的性质、全等三角形的判定,解题的关键是熟练掌握全等三角形的判定以及正方形的性质,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知方程x2-6x+4=0的两根是x1,x2,则x1+x2的值是( )
| A. | 6 | B. | -6 | C. | 4 | D. | -4 |
7.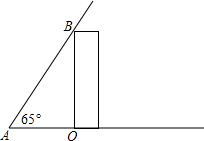 如图,为测量一幢大楼的高度,在地面上距离楼底O点30m的点A处,测得楼顶B点的仰角∠OAB=65°,则这幢大楼的高度为( )m.
如图,为测量一幢大楼的高度,在地面上距离楼底O点30m的点A处,测得楼顶B点的仰角∠OAB=65°,则这幢大楼的高度为( )m.
 如图,为测量一幢大楼的高度,在地面上距离楼底O点30m的点A处,测得楼顶B点的仰角∠OAB=65°,则这幢大楼的高度为( )m.
如图,为测量一幢大楼的高度,在地面上距离楼底O点30m的点A处,测得楼顶B点的仰角∠OAB=65°,则这幢大楼的高度为( )m.| A. | 30•sin65° | B. | $\frac{30}{cos65°}$ | C. | 30•tan65° | D. | $\frac{30}{tan65°}$ |
4.下列四个命题:
①垂直于弦的直径平分弦所对的两条弧;
②在同圆或等圆中,相等的弦所对的圆 周角相等;
③三角形有且只有一个外接圆;
④任意三角形是内心总是在三角形的内部;
⑤三角形的外心到三角形三边的距离相等.
其中真命题的个数有( )
①垂直于弦的直径平分弦所对的两条弧;
②在同圆或等圆中,相等的弦所对的圆 周角相等;
③三角形有且只有一个外接圆;
④任意三角形是内心总是在三角形的内部;
⑤三角形的外心到三角形三边的距离相等.
其中真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1. 一次函数y=kx+b的图象如图,则当0<x≤1时,y的范围是( )
一次函数y=kx+b的图象如图,则当0<x≤1时,y的范围是( )
 一次函数y=kx+b的图象如图,则当0<x≤1时,y的范围是( )
一次函数y=kx+b的图象如图,则当0<x≤1时,y的范围是( )| A. | y>0 | B. | -2<y≤0 | C. | -2<y≤1 | D. | 无法判断 |
 如图,△OCD是由△OAB旋转得到的,∠AOC=30°则∠BOD=30°.
如图,△OCD是由△OAB旋转得到的,∠AOC=30°则∠BOD=30°.