题目内容
20.已知2+$\frac{2}{3}$=22×$\frac{2}{3}$,3+$\frac{3}{8}$=32×$\frac{3}{8}$,4+$\frac{4}{15}$=42×$\frac{4}{15}$,…
若10+$\frac{a}{b}$=102×$\frac{a}{b}$(a,b为正整数),求分式$\frac{{a}^{2}+2ab+{b}^{2}}{a-b}$÷$\frac{a+b}{a-b}$•(b-9a)3的值.
分析 先根据分式混合运算的法则把原式进行化简,由题意找出规律求出a,b的值,代入代数式进行计算即可.
解答 解:原式=$\frac{(a+b)^{2}}{a-b}$•$\frac{a-b}{a+b}$•(b-9a)3
=(a+b)•(b-9a)3.
∵2+$\frac{2}{3}$=22×$\frac{2}{3}$=22×$\frac{2}{{2}^{2}-1}$,3+$\frac{3}{8}$=32×$\frac{3}{8}$=32×$\frac{3}{{3}^{2}-1}$,4+$\frac{4}{15}$=42×$\frac{4}{15}$=42×$\frac{4}{{4}^{2}-1}$,10+$\frac{a}{b}$=102×$\frac{a}{b}$,
∴a=10,b=102-1=99,
∴原式=(10+99)•(99-9×10)3=109×93=79461.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.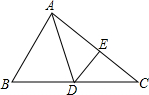 如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )
如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )
 如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )
如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,那么点D到AB的距离是( )| A. | $\frac{10}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{6}{5}$ | D. | 2 |