题目内容
3.在一个不透明的盒子里,装有四个分别标有数字-2,-4,0,6的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.(1)求小明、小华各取一次小球所确定的点(x,y)落在二次函数y=x2+x-2的图象上的概率;
(2)求小明、小华各取一次小球所确定的数x、y满足y>x2+x-2的概率.
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小明、小华各取一次小球所确定的点(x,y)落在二次函数y=x2+x-2的图象上的情况,再利用概率公式即可求得答案;
(2)由(1)可求得小明、小华各取一次小球所确定的数x、y满足y>x2+x-2的情况,再利用概率公式即可求得答案.
解答 解:(1)画树状图得:
∵共有16种等可能的结果,点(x,y)落在二次函数y=x2+x-2的图象上的有(-2,0),(0,-2),
∴小明、小华各取一次小球所确定的点(x,y)落在二次函数y=x2+x-2的图象上的概率为:$\frac{3}{16}$;
(2)∵所确定的数x、y满足y>x2+x-2的有(-2,6),(0,0),(0,6),
∴小明、小华各取一次小球所确定的数x、y满足y>x2+x-2的概率为:$\frac{3}{16}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.将抛物线$y=-\frac{1}{2}{x^2}$+2x+1的顶点坐标为( )
| A. | (2,3) | B. | (-2,-3) | C. | (-2,-1) | D. | (2,-3) |
8.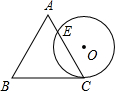 如图,一个边长为a的等边三角形ABC的高与⊙O的直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则AE:EC的值为( )
如图,一个边长为a的等边三角形ABC的高与⊙O的直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则AE:EC的值为( )
 如图,一个边长为a的等边三角形ABC的高与⊙O的直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则AE:EC的值为( )
如图,一个边长为a的等边三角形ABC的高与⊙O的直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则AE:EC的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
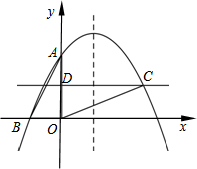 如图,在平面直角坐标系中,一条抛物线经过点A(0,2)、B(-1,0),且对称轴为直线x=1.点C是抛物线上x轴上方任意一点,直线CD平行于x轴,与y轴交于点D.设点C的横坐标为x.
如图,在平面直角坐标系中,一条抛物线经过点A(0,2)、B(-1,0),且对称轴为直线x=1.点C是抛物线上x轴上方任意一点,直线CD平行于x轴,与y轴交于点D.设点C的横坐标为x.

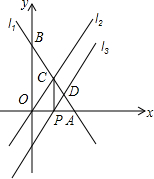 如图,已知直线l1:y=-2x+8与两坐标轴分别相交于A、B两点,与直线l2:y=2x相交于点C,点P为x轴上的一个动点,过点P的直线,l3∥l2,且与l1相交于点D.
如图,已知直线l1:y=-2x+8与两坐标轴分别相交于A、B两点,与直线l2:y=2x相交于点C,点P为x轴上的一个动点,过点P的直线,l3∥l2,且与l1相交于点D.