题目内容
16.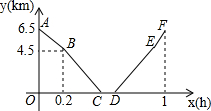 从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小明出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.
从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小明出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.(1)小明骑车在平路上的速度为15km/h,他在乙地休息了0.1h.
(2)分别求线段AB、EF所对应的函数关系式.
(3)从甲地到乙地经过丙地,如果小明两次经过丙地的时间间隔为0.85h,求丙地与甲地之间的路程.
分析 (1)分别计算出小明骑车上坡的速度,小明平路上的速度,小明下坡的速度,小明平路上所用的时间,小明下坡所用的时间为,即可解答;
(2)根据上坡的速度为10km/h,下坡的速度为20km/h,所以线段AB所对应的函数关系式为:y=6.5-10x,线段EF所对应的函数关系式为y=4.5+20(x-0.9),即可解答;
(3)设小明出发a小时第一次经过丙地,根据题意得到6.5-10a=20(a+0.85)-13.5,求出a的值,即可解答.
解答 解:(1)小明骑车上坡的速度为:(6.5-4.5)÷0.2=10(km/h),
小明平路上的速度为:10+5=15(km/h),
小明下坡的速度为:15+5=20(km/h),
小明平路上所用的时间为:2(4.5÷15)=0.6h,
小明下坡所用的时间为:(6.5-4.5)÷20=0.1h
所以小明在乙地休息了:1-0.1-0.6-0.2=0.1(h).
故答案为:15,0.1;
(2)由题意可知:上坡的速度为10km/h,下坡的速度为20km/h,
所以线段AB所对应的函数关系式为:y=6.5-10x,
即y=-10x+6.5(0≤x≤0.2).
线段EF所对应的函数关系式为y=4.5+20(x-0.9).
即y=20x-13.5(0.9≤x≤1).
(3)由题意可知:小明第一次经过丙地在AB段,第二次经过丙地在EF段,
设小明出发a小时第一次经过丙地,
则小明出发后(a+0.85)小时第二次经过丙地,
6.5-10a=20(a+0.85)-13.5
解得:a=$\frac{1}{10}$.
$\frac{1}{10}×10$=1(千米).
答:丙地与甲地之间的路程为1千米.
点评 本题考查了一次函数的应用,解决本题的关键是读懂函数图象,求出一次函数的解析式.

 名师点拨卷系列答案
名师点拨卷系列答案| x | … | -2 | 0 | 2 | 4 | … |
| y=kx+b | … | 3 | -1 | m | n | … |
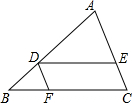 如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )
如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )| A. | $\frac{AD}{DB}$=$\frac{DE}{BF}$ | B. | $\frac{DE}{BC}$=$\frac{AE}{AC}$ | C. | $\frac{AE}{CE}$=$\frac{BF}{CF}$ | D. | $\frac{CE}{AC}$=$\frac{BF}{BC}$ |
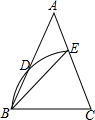 如图,在△ABC中,AB=AC,∠A=32°,以点C为圆心,BC长为半径作弧,交AB于点D,交AC于点E,连结BE,则∠ABE的大小为21度.
如图,在△ABC中,AB=AC,∠A=32°,以点C为圆心,BC长为半径作弧,交AB于点D,交AC于点E,连结BE,则∠ABE的大小为21度. 作图题(只保留作图痕迹,不写作法)
作图题(只保留作图痕迹,不写作法)